Золотий трикутник (геометрія)
Золотий трикутник[1] — рівнобедрений трикутник, у якому бічні сторони знаходиться у золотому перетині до основи:

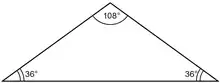
Кути
- Кут при вершині[2] дорівнює
- Отже, золотий трикутник — рівнобедрений трикутник з гострим кутом при вершині.
- Оскільки кути трикутника складають , кожен з базових кутів (CBX і CXB) дорівнює:
- Примітка:
- Золотий трикутник однозначно визначений як єдиний трикутник, який має три кути у пропорціях 1: 2: 2 (36 °, 72 °, 72 °).[3]
В інших геометричних фігурах
- Золоті трикутники можна знайти у вершинах правильних пентаграм .
- Золоті трикутники також можна знайти в правильному десятикутнику, рівносторонньому десятигранному багатокутнику, з'єднавши будь-які дві сусідні вершини з центром. Це тому, що: 180 (10-2) / 10 = 144 ° — це внутрішній кут, а поділивши його, маємо: 144/2 = 72 °.[1]
- Також золоті трикутники зустрічаються в розгортках кількох зірок додекаедрів та ікосаедрів .
Логарифмічна спіраль
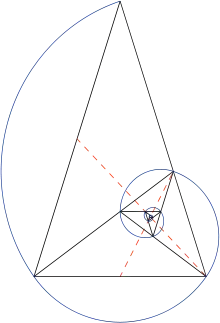
Золотий трикутник використовується для формування деяких точок логарифмічної спіралі . Поділивши один із кутів при основі навпіл, з'являється нова точка, яка, у свою чергу, утворює ще один золотий трикутник.[4] Процес поділу можна продовжувати безліч разів, створюючи нескінченну кількість золотих трикутників. Через вершини можна провести логарифмічну спіраль. Ця спіраль також відома як рівнокутна спіраль, термін, який ввів Рене Декарт . «Якщо від полюса до будь-якої точки кривої проведена пряма лінія, вона перетне криву завжди під одним і тим самим кутом», отже, рівнокутна .[5]
Золотий гномон
.svg.png.webp)
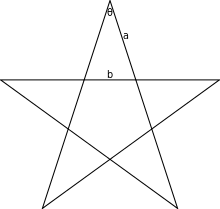
З золотим трикутником тісно пов'язаний золотий гномон, це рівнобедрений трикутник, у якому відношення довжин рівних сторін до довжини основи є оберненим до золотого перерізу .
« У золотому трикутник відношення довжини основи до довжини сторони, дорівнює золотому перерізу φ, тоді як у золотому гномоні відношення довжини сторони до довжини основи, дорівнює золотому перерізу φ.»[6]
Кути
(Відстані AX і CX дорівнюють a '= a = φ, а відстань AC дорівнює b' = φ², як видно на малюнку.)
- Кут при вершині AXC дорівнює:
- Звідси золотий гномон — тупий (рівнобедрений) трикутник.
- Примітка:
- Оскільки кути трикутника AXC складають , кожен з кутів при основі CAX і ACX дорівнює:
- Примітка:
- Золотий гномон однозначно ідентифікується як трикутник, що має три кути у пропорціях 1: 1: 3 (36 °, 36 °, 108 °). Кути при основі його дорівнюють 36 °, що відповідає вершині золотого трикутника.
Бісекція
- Поділивши один з кутів при основі на 2 рівні кути, золотий трикутник можна розділити на золотий трикутник та золотий гномон.
- Поділивши його кут при вершині на 2 кути (один вдвічі більший за інший), золотий гномон може бути поділений на золоті трикутники та золотий гномон.
- Золотий гномон і золотий трикутник з спільною стороною, також називають тупим і гострим трикутниками Робінсона.[3]
Мозаїка Пенроуза
- Ці рівнобедрені трикутники також можна використовувати для виготовлення мозаїки Пенроуза. Плитки Пенроуза утворюються з «зміїв» та «дротиків». Змії утворюються з двох золотих трикутників, а дротик — з двох гномонів.

Див. також
- Золотий прямокутник
- Золотий ромб
- Трикутник Кеплера
- Золотий трикутник Кімберлінга
- Лютня Піфагора
- Пентаграма
Список літератури
- Kimberly Elam. Geometry of Design. — New York : Princeton Architectural Press, 2001. — ISBN 1-56898-249-6.
- H.E. Huntley. The Divine Proportion: A Study In Mathematical Beauty. — New York : Dover Publications Inc, 1970. — ISBN 0-486-22254-3.
- Mario Livio. The Golden Ratio: The Story of Phi, The World's Most Astonishing Number. — Broadway Books, 2002. — ISBN 0-7679-0815-5.
- Arthur Loeb. Concepts and Images: Visual Mathematics. — Boston : Birkhäuser Boston, 1992. — ISBN 0-8176-3620-X.
Примітки
- Elam, Kimberly (2001). Geometry of Design. New York: Princeton Architectural Press. ISBN 1-56898-249-6.
- Weisstein, Eric W. Golden Triangle. mathworld.wolfram.com (англ.). Процитовано 26 грудня 2019.
- Tilings Encyclopedia. 1970. Архів оригіналу за 24 травня 2009.
- Huntley, H.E. (1970). The Divine Proportion: A Study In Mathematical Beauty. New York: Dover Publications Inc. ISBN 0-486-22254-3.
- Livio, Mario (2002). The Golden Ratio: The Story of Phi, The World's Most Astonishing Number. New York: Broadway Books. ISBN 0-7679-0815-5.
- Loeb, Arthur (1992). Concepts and Images: Visual Mathematics. Boston: Birkhäuser Boston. с. 180. ISBN 0-8176-3620-X.
Посилання
- Weisstein, Eric W. Golden triangle(англ.) на сайті Wolfram MathWorld.
- Weisstein, Eric W. Golden gnomon(англ.) на сайті Wolfram MathWorld.
- Трикутники Робінзона в Енциклопедії Тілінга
- Золотий трикутник за Евклідом
- Надзвичайна взаємність золотих трикутників у Тартапелазі Джорджо П'єтрокола