Коефіцієнт кореляції рангу Спірмена
Коефіцієнт кореляції рангу Спірмена — непараметрична міра статистичної залежності між двома змінними; названий на честь Чарльза Спірмена. Він оцінює наскільки добре можна описати відношення між двома змінними за допомогою монотонної функції. Якщо немає повторних значень даних, то коефіцієнт Спірмена дорівнює 1 або −1, це відбувається коли кожна змінна є монотонною функцією від іншої змінної. Коефіцієнт кореляції, як і будь-яке обчислення кореляції, підходить для безперервних та дискретних змінних, у тому числі порядкових.
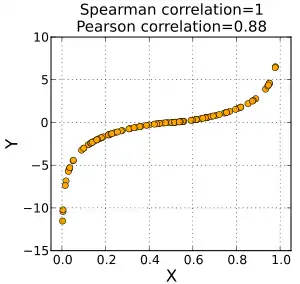
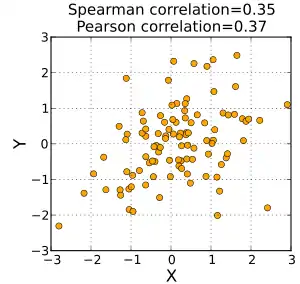
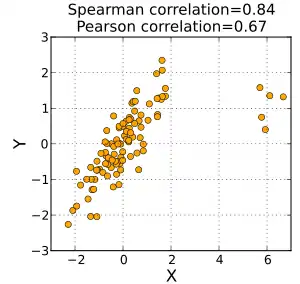
Визначення та розрахунок
Коефіцієнт кореляції Спірмена визначається як коефіцієнт кореляції Пірсона між ранжуванням змінних. Для вибірки обсягу n множини Xi, Yi перетворюються в ряди xi, yi та обчислюється таким чином:
Однаковим значенням (ранг зв'язків або величина дублікатів) присвоюється ранг, що дорівнює середньому числу їхніх позицій в порядку зростанні величини. У наведеній нижче таблиці зверніть увагу, що ранг значень xi при однаковій величині змінної Xi є однаковими:
| Зміна | Позиція в порядку зростання | Ранг |
|---|---|---|
| 0.8 | 1 | 1 |
| 1.2 | 2 | |
| 1.2 | 3 | |
| 2.3 | 4 | 4 |
| 18 | 5 | 5 |
У застосуваннях, де повторювані значення відсутні, для розрахунку може бути використана проста процедура. Різниця між рангами кожного спостереження від двох змінних вираховуються і визначається за формулою: Зауважимо, що цей останній спосіб не слід використовувати в тих випадках, коли набір даних буде скорочуватись, тобто, коли коефіцієнт кореляції Спірмена бажаний для верхнього запису X (або шляхом попереднього зміни положення або після зміни рангу або й те, й інше).
Пов'язані величини
Є кілька інших числових критеріїв, які кількісно визначають ступінь статистичної залежності між парами спостережень. Найбільш поширеним з них є коефіцієнт Пірсона, який є аналогічним до методу кореляції рангу Спірмена, який вимірює «лінійні» співвідношення між значеннями, а не між їхніми рангами. Коефіцієнт кореляції Спірмена та Пірсона в загальному випадку вимірюють різні види взіємозв'язку між величинами (монотонний зв'язок у випадку кореляції Спрмана, лінійний зв'язок у випадку Пірсона) однак за умови коли обидві величени мають спільний гауссовий розподіл коефіцієнт корреляції Спірмана можна перетворити в коефіцієнт кореяції пірсона за допомогою формули Альтернативна назва для рангової кореляції Спірмена є «степінь кореляції», в ній «ранг» зі спостережень замінюється на «степінь». В неперервних розподілах, степінь спостереження, за домовленістю, завжди вдвічі менше, ніж ранг, і, отже, степінь і ранг кореляції по суті одна й таж величина. У більш загальному сенсі «степінь» спостережень пропорційна оцінці частки населення менше заданого значення, при цьому половина спостереження регулюється досліджуваними величинами. Таким чином, це відповідає одній можливій обробці пов'язаних рангів. У той час як незвичайне, термін «степінь кореляції» досі використовується.
Інтерпретація
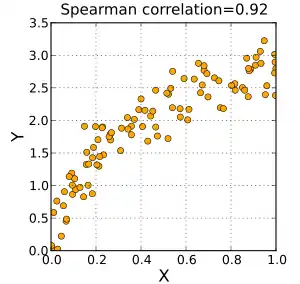 додатній коефіцієнт кореляції Спірмена — відповідає збільшенню монотонності між X і Y. |
 від'ємний коефіцієнт кореляція Спірмена — відповідає монотонному зменшенню між X і Y. |
Знак кореляції Спірмена вказує напрямок зв'язку між Х (незалежною змінною) та Y (залежною змінною). Якщо Y має тенденцію до збільшення, коли Х збільшується, коефіцієнт кореляції Спірмена є додатнім. Якщо Y має тенденцію до зменшення, коли X збільшується, коефіцієнт кореляції Спірмена від'ємний. Коефіцієнт Спірмена рівний нулю вказує на те, що Y не збільшується та не зменшується при збільшенні X. Збільшення коефіцієнта Спірмена відбувається при наближенні величин X та Y один до одного таким чином, що вони можуть стати монотонною функцією один одного. Коли X і Y монотонно пов'язані, коефіцієнт кореляції Спірмена набуває значення 1. Ідеальне монотонне зростання співвідношення передбачає, що для будь-яких двох пар значень даних (xi, yi) та (xj, yj): xi- xj та yi- yj завжди мають однаковий знак. Ідеальне монотонно спадне співвідношення передбачає, що xi- xj та yi- yj завжди мають протилежні знаки. Коефіцієнт кореляції Спірмена часто описується як «непараметричний». Це може мати два значення. По-перше, той факт, що найкращі результати повної кореляції Спірмена які бувають тоді, коли X та Y пов'язані будь-якою монотонною функцією, можна порівняти з кореляцією Пірсона, яка приймає найкраще значення лише коли X та Y зв'язані лінійною функцією. По-друге, кореляція Спірмена є непараметричною в тому сенсі, що його точний розподіл вибірки може бути отриманий без необхідності відомостей про параметри спільного розподілу вірогідності X та Y.
Приклад
У цьому прикладі ми будемо використовувати вихідні дані в таблиці, щоб обчислити кореляцію між IQ людини з кількістю годин, проведених перед телевізором на тиждень.
| IQ, | Години, проведені за телевізором — |
| 106 | 7 |
| 86 | 0 |
| 100 | 27 |
| 101 | 50 |
| 99 | 28 |
| 103 | 29 |
| 97 | 20 |
| 113 | 12 |
| 112 | 6 |
| 110 | 17 |
По-перше, ми повинні знайти значення . Для цього ми зробимо наступні кроки, відображені в таблиці нижче:
1. Сортування даних першої колонки (). Створення нової колонки і привласнити його ранжируваних значень 1,2,3, … N.
2. Далі, сортування даних другої колонки (). Створення четвертої колонки і так само присвоїти їй ранжируваних значень 1,2,3, … N.
3. Створення п'ятої колонки , що є різницею двох стовпців рангу ( та ).
4. Створення останнього стовпця для зберігання значення стовпця у квадраті.
| IQ, | Години, проведені за телевізором | ранг | ранг | ||
| 86 | 0 | 1 | 1 | 0 | 0 |
| 97 | 20 | 2 | 6 | −4 | 16 |
| 99 | 28 | 3 | 8 | −5 | 25 |
| 100 | 27 | 4 | 7 | −3 | 9 |
| 101 | 50 | 5 | 10 | −5 | 25 |
| 103 | 29 | 6 | 9 | −3 | 9 |
| 106 | 7 | 7 | 3 | 4 | 16 |
| 110 | 17 | 8 | 5 | 3 | 9 |
| 112 | 6 | 9 | 2 | 7 | 49 |
| 113 | 12 | 10 | 4 | 6 | 36 |
Коли знайдено , ми можемо знайти . n=10 . Таким чином, тепер ці значення можна підставити в рівняння:
де ρ = -29/165 = −0.175757575…
ρ- рівень (статистична значущість) дорівнює 0,68640058 (використали t розподіл Стьюдента).
Таке невелике значення показує, що кореляція між IQ та годинами, проведеними за телевізором дуже низька. У випадку коли вихідні значення пов'язані — ця формула не може бути використана. Замість коефіцієнта кореляції Персона повинні бути пораховані ранги.
Визначення терміну
Один з підходів до тестування: наскільки спостережуване значення ρ значно відрізняється від нуля (г завжди в діапазоні −1 ≤ г ≤ 1) — це обчислення ймовірності того, що значення ρ було б більше або дорівнює змінній г, враховуючи нульову гіпотезу, за допомогою тесту перестановки. Перевагою цього підходу є те, що він автоматично враховує кількість прив'язаних значень даних, що є в зразку, і способі, яким розглядали при обчисленні рангу кореляції. Інший підхід паралельно використовує перетворення Фішера у розумінні коефіцієнта кореляції Персона. Тобто, довірчий інтервал та перевірка гіпотези, пов'язаних з значенням можуть бути знайдені за допомогою перетворення Фішера:
Якщо F(r) є перетворенням Фішера для r, то для коефіцієнта кореляції рангу Спірмена та n — розміру вибірки справедливо :
Це є z — значення для r, які приблизно наближується до нормального розподілу в нульовій гіпотезі статистичної незалежності (ρ=0). Можна також перевірити на використання значення:
яка поширюється приблизно як t-розподіл Стьюдента з ступенями свободи при нульовій гіпотезі. Обґрунтування цього результату залежить від перестановки аргументів. Узагальненням коефіцієнта Спірмена корисно використовувати в ситуаціях, коли є три або більше умов, ряд спостережуваних суб'єктів та відомо, що спостереження матимуть певний порядок. Наприклад, ряду суб'єктів може бути дано три випробування з використанням однакових завдань, і це передбачає, що від випробування до випробування буде відбуватися поліпшення якості виконання. Тест значущості тенденції між умовами в такій ситуації був розроблений E. B. Page[1] і, як правило, називається тестом Пейджа для тенденцій між упорядкованими альтернативами.
Посилання
- Page, E. B. (1963). Ordered hypotheses for multiple treatments: A significance test for linear ranks. Journal of the American Statistical Association 58 (301): 216–230. JSTOR 2282965. doi:10.2307/2282965.