Крива Мура
Крива Мура — фрактальна крива, що заповнює простір і є варіантом кривої Гільберта. Була запропонована в 1900 р. американським математиком Еліакимом Гастінгсом Муром (E.H. Moore)[1].
Властивості
Розмірність Гаусдорфа кривої Мура дорівнює (її образ є одиничним квадратом, розмірність якого дорівнює 2 при будь-якому визначенні розмірності, а її граф є компактною множиною, гомеоморфною замкнутому одиничному інтервалу з розмірністю Гаусдорфа 2) .
є -м наближенням до граничної кривої. Евклідова довжина кривої дорівнює , тобто росте експоненціально з , в той же час сама крива завжди лишається в межах квадрата з скінченною площею.
Ітерації кривої Мура

Представлення в системі Лінденмаєра
Криву Мура можливо описати в L-системі:
- Alphabet: L, R
- Constants: F, +, −
- Axiom: LFL+F+LFL
- Production rules:
- L → −RF+LFL+FR−
- R → +LF−RFR−FL+
Тут F означає «йдемо вперед», + означає «повертаємо вліво на 90°», а − позначає «поворот направо на 90°».
3D-узагальнення
Крива Мура третього порядку у тривимірному просторі:
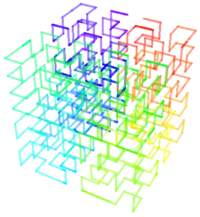
Напрями використання
На основі кривої Мура можуть бути реалізовані вібраторні або друковані конструкції фрактальних антен[1], які за своїми характеристиками досить близькі до антен на основі кривої Гільберта[1].
Див. також
Примітки
- Слюсар, В. (2007). Фрактальные антенны. Принципиально новый тип «ломаных» антенн. Часть 2.. Электроника: наука, технология, бизнес. — 2007. — № 6. с. С. 85.
Література
- Moore E.H. On certain crinkly curves.– Trans. Amer. Math. Soc. 1900, N1, p. 72 — 90.
- A. Bogomolny. Plane Filling Curves from Interactive Mathematics Miscellany and Puzzles. — 2008.