Фрактал

Фракта́л (від лат. fractus — подрібнений, дробовий) — у побутовому розумінні часто означають як деяку нерегулярну, самоподібну структуру. Більш строге означення фрактала вимагає глибоких знань із курсів алгебри і математичного аналізу. Поширеним є розуміння фрактала як множини, яка має властивість самоподібності, тобто такої множини, що складається з частин, які є подібними до неї самої.[1]

Границя множини Мандельброта є відомим прикладом фрактала

Однак, слід зауважити, що не всі самоподібні множини є фрактальними і не всі фрактальні множини є самоподібними. Наприклад, будь-який відрізок є самоподібною множиною, але водночас він не є фракталом. Водночас існують фрактальні множини, які не є самоподібними.[2]

Термін фрактал увів 1975 року французький математик Бенуа Мандельброт у своїй книжці «Фрактали: випадок, форма, розмірність» (перекладена англійською в 1977 році).[1]

Історія
Сніжинка Коха є межею нескінченної конструкції, що починається з трикутника та доповнюється рекурсивною заміною кожного сегменту набором із чотирьох сегментів, які утворюють трикутний «виступ». Щоразу, коли додаються нові трикутники (при ітерації), периметр фігури зростає на третину й тому прямує до нескінченності, коли кількість ітерацій прямує до нескінченності. Довжина межі сніжинки Коха, таким чином, є нескінченною, а її площа — скінченною.

Об'єкти, які виникають під час побудови фракталів, досліджувались задовго до того, як виник сам термін «фрактал». У етноматематиці, наприклад в роботах Рона Еглаша «Африканські Фрактали»[3], задокументовано поширені нині геометричні фігури, які виникають при побудові фракталів, у мистецтві тубільців. У 1525 році німецький митець Альбрехт Дюрер опублікував свою працю Керівництво Художника[4], один із розділів якої має назву «Черепичні шаблони, утворені пентагонами». Пентагон Дюрера багато в чому є схожим на килим Серпінського, але замість квадратів використовуються п'ятикутники. Джексон Поллок (американський експресіоніст 50-х років минулого століття) малював об'єкти, дуже схожі на ті, що виникають при побудові фракталів.[5]

Ідею «рекурсивної самоподібності» було висунуто філософом Ляйбніцом, який також розробив багато з деталей цієї ідеї.[6] В 1872 Карл Веєрштрасс побудував приклад функції з неінтуїтивною особливістю, скрізь неперервною, але усюди недиференційованою — графік цієї функції тепер би називався фракталом.[7] У 1904 Гельґе фон Кох, незадоволений занадто абстрактним та аналітичним означенням Веєрштрасса, розробив більш геометричне означення схожої функції, яка тепер має назву сніжинки Коха. Ідею самоподібних кривих було далі розвинено Полем П'єром Леві, який у своїй роботі Криві та поверхні на площині та у просторі, які складаються із частин, схожих на ціле, виданій 1938 року, описав нову фрактальну криву, відому тепер як Крива Леві.[6]

Георг Кантор навів приклади підмножин дійсних чисел із незвичними властивостями — ці множини Кантора тепер також визнаються як фрактали. Ітераційні функції на комплексній площині досліджувались в кінці 19 та на початку 20 століття Анрі Пуанкаре, Феліксом Кляйном, П'єром Фату та Ґастоном Жюліа. Проте за браком сучасної комп'ютерної графіки у них забракло засобів відобразити красу багатьох із відкритих ними об'єктів.[8]

В 1960-х роках, Бенуа Мандельброт почав дослідження самоподібності в своїх роботах, наприклад «Яка довжина узбережжя Британії? Статистична самоподібність та дробова розмірність». Ця доповідь базувалась на ранніх роботах Луі Фрая Річардсона. В 1975 році Мандельброт використав слово фрактал як назву для об'єктів, розмірність Гаусдорфа яких є більшою за топологічну розмірність.[9] Він проілюстрував своє математичне означення захопливими зображеннями, зробленими за допомогою комп'ютера. Ці зображення привернули велику увагу; багато з них базувалися на рекурсії, що призвело до появи поширеного розуміння слова фрактал.[1][2][9]

Приклади
Множина Жюліа, фрактал, близький до множини Мандельброта.

Порівняно простий клас прикладів фракталів утворюють множини Кантора. Власне, сам Георг Кантор у своїй статті «Про потужність однієї досконалої множини точок»[10] навів приклад лише однієї множини (нині її називають класичною множиною Кантора C0) і довів її континуальність. Аналітично класичну множину Кантора можна задати як множину точок одиничного інтервалу [0;1], у трійковому записі яких відсутня цифра 2.[2] Ця множина є самоподібною, оскільки її можна представити як об'єднання двох множин, кожна з яких подібна до всієї множини з коефіцієнтом 1/3. Топологічна розмірність класичної множини Кантора C0 дорівнює нулю, а розмірність Гаусдорфа дорівнює log 2/log 3, а отже, вона є фракталом.[2]

Якщо розглядати множини точок одиничного інтервалу, запис яких у системі числення з основою N не міститиме однієї чи кількох цілком визначених цифр, можна отримати узагальнення класичної множини Кантора, які мають аналогічні властивості, зокрема, вони також є самоподібними фракталами, розмірність яких обчислюється аналогічно до розмірності множини C0. Наприклад, множина всіх чисел одиничного інтервалу [0;1], запис котрих не містить цифри 7 із їх десяткового подання, є самоподібною фрактальною множиною, розмірність розмірність Гаусдорфа якої дорівнює log 9/log 10.[2]

Також до прикладів фракталів належить фрактал Ляпунова, трикутник Серпінського,[11] килим Серпінського, губка Менгера, сітка Аполлонія, крива дракона, крива заповнення простору, межі множин груп Кліні та крива Коха.[9] Фрактали можуть бути детермінованими або стохастичними (наприклад, недетермінованими).[12]

Хаотичні динамічні системи іноді асоціюються з фракталами (дивіться атрактор).[13] Об'єкти в просторі параметрів, що задають динамічну систему, також можуть бути фракталами. Цікавим прикладом є множина Мандельброта.[12] Ця множина містить у собі цілі круги, тому її розмірність Гаусдорфа дорівнює топологічній розмірності, яка дорівнює 2. Отже, формально множина Мандельброта не є фракталом, але розмірність Гаусдорфа її межі також дорівнює 2 (а топологічна розмірність дорівнює 1). Це було доведено японським математиком Міцухіро Шішікурою в 1991 році.[14] Множини, розмірність Гаусдорфа яких на одиницю більша за їх топологічну розмірність, називають суперфракталами.[2]

Самоподібні множини з незвичайними властивостями в математиці

Починаючи з кінця XIX століття, в математиці з'являються приклади самоподібних об'єктів з патологічними з точки зору класичного аналізу властивостями. До них можна віднести наступні:

Рекурсивна процедура для побудови фрактальних кривих

Існує проста рекурсивна процедура для побудови фрактальних кривих на площині. Задамо довільну ламану зі скінченним числом ланок, яку називають генератором фрактальної кривої. Далі, замінимо в ній кожен відрізок на генератор (точніше, ламаною, подібною до генератора). У цій ламаній знову замінимо кожний відрізок на генератор. Продовжуючи цей процес до нескінченності, як границю (граничну множину) одержимо фрактальну криву.

Прикладами таких кривих є :

За допомогою схожої процедури можна побудувати дерево Піфагора.[21]

Стохастичні фрактали

Природні об'єкти часто мають фрактальну форму. Для їх моделювання можуть застосовуватися стохастичні (випадкові) фрактали. Приклади стохастичних фракталів:

Фрактальна розмірність межі кривої Коха

Наведений нижче аналіз Сніжинки Коха є прикладом того, як самоподібність може використовуватись для аналізу властивостей фрактала.

Загальна довжина N малих сходинок L дорівнює добуткові NL. При застосуванні до сніжинки Коха отримуємо невизначене число, коли L прямує до 0. Але таке означення не є задовільним, оскільки різні криві Коха мають різні розміри. Вихід полягає в тому, щоб вимірювати ані в метрах (m), ані в квадратних метрах (m2), але в деякому іншому ступені метра, mx. Тепер 4N(L/3)x = NLx, оскільки втричі коротший відрізок потребує в 4 рази більше відрізків, як це видно з малюнку. Єдиним розв'язком цього рівняння є x = (log 4)/(log 3) ≈ 1.26186. Тому, одиниця вимірювання довжини межі сніжинки Коха дорівнює приблизно m1.26186.

Генерування фракталів
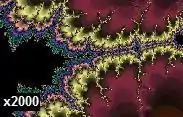Навіть збільшення в 2000 разів розкриває деталі множини Мандельброта, які відтворюють всю множину.

Три поширені методи генерування фракталів:

Класифікація фракталів

Фрактали також можна класифікувати відповідно до їхньої самоподібності. Розрізняють три типи самоподібності у фракталах:

  • Точна самоподібність — Це найсильніший тип самоподібності; фрактал виглядає однаково при різних збільшеннях. У фракталів, згенерованих з використанням ітераційних функцій, часто виявляється точна самоподібність.
  • Майже самоподібність — Слабка форма самоподібності; фрактал виглядає приблизно (але не точно) самоподібним при різних збільшеннях. Майже самоподібні фрактали містять малі копії цілого фрактала у перекручених та вироджених формах. Фрактали, згенеровані з використанням рекурентних відношень, зазвичай є майже (але не точно) самоподібними.
  • Статистична самоподібність — Це найслабкіша форма самоподібності; фрактал має чисельні або статистичні міри, що зберігаються при збільшенні. Найприйнятніші означення «фракталів» просто містять в собі деякий вид статистичної самоподібності (розмірність фрактала, сама по собі, є чисельною мірою, що зберігається при збільшенні). Ймовірнісні фрактали є прикладами фракталів, які є статистично, але не майже й не точно самоподібними.

Слід зазначити, що не всі самоподібні об'єкти є фракталами; наприклад, числова вісь (евклідова пряма) є точно самоподібною, але, оскільки її розмірність Гаусдорфа та топологічна розмірність дорівнюють одиниці, вона не є фракталом.

Об'єкти, що володіють фрактальними властивостями, в природі

У живій природі:

У неживій природі:

Фрактальна папороть, обчислена з використанням системи ітераційних функцій.

Дерева та папороті є фрактальними за своєю природою та можуть моделюватись на комп'ютерах із використанням рекурсивних алгоритмів. Таку рекурсивність ясно видно на таких прикладах: гілка дерева або фронд від папороті є мініатюрним відтворенням цілого; не ідентичне, але схоже за природою.

Поверхня гір може моделюватись на комп'ютері з використанням фракталів: починати з трикутника в тривимірному просторі та з'єднати центральні точки кожного ребра відрізками, отримуючи 4 трикутники. Центральні точки потім зсуваються догори або донизу на випадкову відстань у фіксованому діапазоні. Процедура повторюється зі зменшенням діапазону на кожній ітерації вдвічі. Рекурсивна природа алгоритму гарантує, що ціле є статистично подібним до кожної з деталей.

  • При розриві двох вкритих клеєм листів акрилу утворюється фрактальний візерунок.
  • Високовольтний розряд в 4″ блоці акрилу створює фрактальний рисунок Ліхтенберга.
  • Фрактальні тріщини з'являються на DVD диску після обробки мікрохвильовим випроміненням.
  • Капуста Romanesco broccoli демонструє дуже дрібні природні фрактали.
  • Ö-фрактал

Об'єкти, що володіють фрактальними властивостями, в літературі

Польські фізики з Краківської політехніки, проаналізувавши довжину речень у 113 великих творах світової літератури різних епох, написаних різними мовами й різними авторами (Оноре де Бальзак, Вільям Шекспір, Вірджинія Вулф, Томас Манн, Умберто Еко, Федір Достоєвський, Генрик Сенкевич, Джон Толкін, Хуліо Кортасар), виявили в них фігуру, малі частини якої при довільному збільшенні є подібними до неї самої. Ці фігури — самоподібні навіть на множинних рівнях. Всі досліджені твори демонструють самоподібності в послідовності та довжині речень.

Особливо складними виявилися роман Джеймса Джойса «Поминки за Фіннеганом» і Старий Заповіт.[22][23]

Застосування

Природничі науки

У фізиці фрактали природним чином виникають при моделюванні нелінійних процесів, таких, як турбулентний плин рідини, складні процеси дифузії — адсорбції, полум'я, хмари тощо Фрактали використовуються при моделюванні пористих матеріалів, наприклад, в нафтохімії. У біології вони застосовуються для моделювання популяцій і для опису систем внутрішніх органів (система кровоносних судин). Після створення кривої Коха було запропоновано використовувати її при обчисленні протяжності берегової лінії.

Генерація зображень природних об'єктів
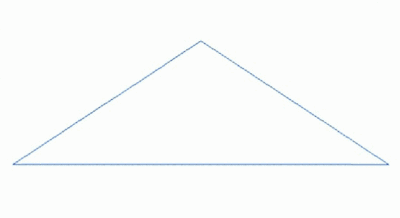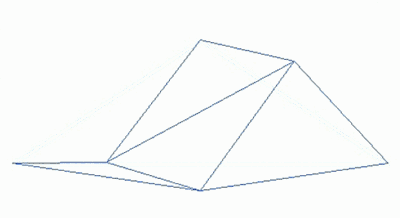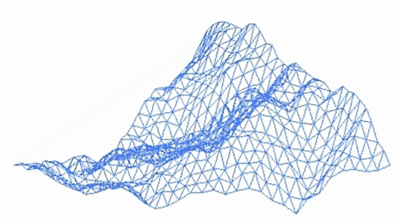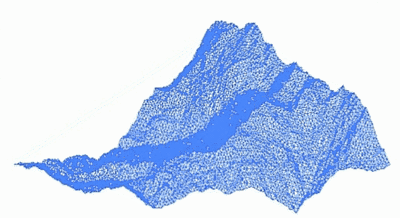
Фрактал, який моделює поверхню гори (анімація).

Геометричні фрактали застосовуються для отримання зображень дерев, кущів, берегових ліній тощо. Алгебричні та стохастичні — для побудови ландшафтів, поверхні морів, моделей біологічних та інших об'єктів.

Механіка рідин

Фракталами добре описуються такі процеси та явища, що стосуються механіки рідин і газів:

Біологія

Фрактальні антени

Фрактальну геометрію для проектування антенних пристроїв було вперше застосовано американським інженером Натаном Коеном, який тоді жив у центрі Бостона, де було заборонено встановлювати зовнішні антени на будинках. Натан вирізав з алюмінієвої фольги фігуру у формі кривої Коха та наклеїв її на аркуш паперу, а потім приєднав до приймача. Виявилось, що така антена працює не гірше за звичайну.[24][19][25][26]

Це дозволило Коену заснувати власну компанію й налагодити серійний випуск антен своєї конструкції. З тих пір такі антени отримали інтенсивний розвиток[19][25][26][27][28] Перевагами фрактальних антен є багатодіапазонність та широкосмуговість.

Стиснення зображень

За допомогою фракталів можна стискати великі растрові зображення до частин їхніх нормальних розмірів. Це твердження випливає з теореми Банаха про стискуючі відображення й є результатом роботи дослідника Технологічного інституту шт. Джорджія Майкла Барнслі.

Коротко метод можна описати таким чином. Зображення кодується кількома простими перетвореннями (в нашому випадкові афінними), тобто визначається коефіцієнтами цих перетворень (в нашому випадкові: A, B, C, D, E та F).

Наприклад, закодувавши якесь зображення двома афінними перетвореннями, ми однозначно визначаємо його за допомогою 12 коефіцієнтів. Якщо тепер задати яку-небудь початкову точку (наприклад, X = 0, Y = 0) та запустити ітераційний процес, то ми після першої ітерації отримаємо дві точки, після другої — чотири, після третьої — вісім і т. д. Через кілька десятків ітерацій сукупність отриманих точок описуватиме закодоване зображення. Але проблема полягає в тому, що дуже важко знайти коефіцієнти перетворень, які кодували б довільне зображення.

Не зважаючи на те, що було створено програмне забезпечення, що реалізує ці алгоритми (наприклад, бібліотеки фрактального стиснення використовуються в Microsoft Encarta), досить ефективного методу не було знайдено досі, а сам Майкл Барнслі продовжує працювати в даному напрямкові.

Децентралізовані мережі

Система призначення IP-адрес в мережі Netsukuku використовує принцип фрактального стиснення інформації для компактного зберігання інформації про вузли мережі. Кожен вузол мережі Netsukuku тримає лише 4 Кб інформації про стан сусідніх вузлів, при цьому будь-який новий вузол під'єднується до загальної мережі без необхідності в центральному регулюванні роздавання IP-адрес, що, наприклад, є характерним для мережі Інтернет. Таким чином, принцип фрактального стиснення гарантує повністю децентралізовану, а отже, максимально стійку роботу всієї мережі.

Див. також

Примітки
  1. Mandelbrot, Benoît (1977). Fractals: Form, chance, and dimension (англійська). San-Francisco: Freeman. с. 346. ISBN 0716704730.
  2. Працьовитий, Микола (1998). Фрактальний підхід у дослідженнях сингулярних розподілів (українська). Київ: НПУ імені М.П.Драгоманова. с. 296. ISBN 966-7584-05-4.
  3. Eglash, Ron (2005). African fractals : modern computing and indigenous design (англійська). New Brunswick, N.J.: Rutgers University Press. ISBN 0-8135-2613-2.
  4. Дюрер, Альбрехт (2011). Трактати (переклад з німецької) (російська). Москва: Видавництво студії Артемія Лєбєдєва. с. 264.
  5. Азаренко, Наталья (3 серпня 2017). Картины, которые снимут стресс: фракталы в живописи. Artchive. Процитовано 10 червня 2021.
  6. Pickover, Clifford A. (2009). The Math Book: From Pythagoras to the 57th Dimension, 250 Milestones in the History of Mathematics (англійська). Sterling Publishing Company, Inc. с. 527. ISBN 9781402757969.
  7. Вейєрштрасс, Карл (1872). Über continuirliche Functionen eines reellen Arguments, die für keinen Werth des Letzteren einen bestimmten Differentialquotienten besitzen (німецька).
  8. Fractal Geometry. web.archive.org. 12 березня 2012. Процитовано 10 червня 2021.
  9. Mandelbrot, Benuit (1983). The fractal geometry of nature (англійська). New York: Freeman. с. 540. ISBN 0716711869.
  10. Cantor, Georg. On the Power of Perfect Sets of Points (De la puissance des ensembles parfait de points), Acta Mathematica 4 (1884) 381--392.
  11. Sierpinski, Waclaw. Sur une courbe dont tout point est un point de ramification // Comptes rendus hebdomadaires des séances de l'Académie des sciences. - Paris. – Tome 160, Janvier - Juin 1915. - Pp. 302 – 305.
  12. Peitgen Heinz-Otto, Peter H. Richter (1986). The Beauty of Fractals: Images of Complex Dynamical Systems (англійська). Springer. с. 176. ISBN 3642617190.
  13. Katok, A. B. (1995). Introduction to the modern theory of dynamical systems. Cambridge ; New York, NY : Cambridge University Press. ISBN 978-0-521-34187-5.
  14. Shishikura, Mitsuhiro (1991). The Hausdorff dimension of the boundary of the Mandelbrot set and Julia sets // Annals of mathematics. Vol.147-2. P. 225-267 (англійська).
  15. Gazale, Midhat (1999). Gnomon: from pharaons to fractals (англійська). New Jersey: Princeton University Press. с. 272. ISBN 9780691005140.
  16. Menger, Karl (1926). "Allgemeine Räume und Cartesische Räume. I.", Communications to the Amsterdam Academy of Sciences. English translation reprinted in Edgar, Gerald A., ed. (2004), Classics on fractals, Studies in Nonlinearity (англійська). Westview Press. Advanced Book Program, Boulder, CO. ISBN 978-0-8133-4153-8.
  17. Peano, G. (1 березня 1890). Sur une courbe, qui remplit toute une aire plane. Mathematische Annalen (фр.) 36 (1). с. 157–160. ISSN 1432-1807. doi:10.1007/BF01199438. Процитовано 12 червня 2021.
  18. Фракталы в физике. Труды 6-го международного симпозиума по фракталам в физике. Москва: Мир. 1988. с. 672.
  19. Слюсар, В. (2007). Фрактальные антенны. Принципиально новый тип «ломаных» антенн.. Электроника: наука, технология, бизнес. — 2007. — № 5. с. С. 78—83.
  20. Hilbert, David (1891). Ueber die stetige Abbildung einer Linie auf ein Flächenstück. Mathematische Annalen (нім.) 38. с. 459–460. ISSN 0025-5831. Процитовано 12 червня 2021.
  21. Weisstein, Eric W. Pythagoras Tree. mathworld.wolfram.com (англ.). Процитовано 12 червня 2021.
  22. Henryk Niewodniczanski. In Weltliteratur verstecken sich Fraktale. // Scinexx.de, 22.01.2016 (нім.)
  23. Фрактали в світовій літературі. // Zbruch, 26.01.2016
  24. Слюсар В. И. Фрактальные антенны. // Радиоаматор. — 2002. — № 9. — С. 54 -56., Конструктор. — 2002. — № 8. — С. 6 — 8.
  25. Слюсар, В. (2007). Фрактальные антенны. Принципиально новый тип «ломаных» антенн. Часть 2.. Электроника: наука, технология, бизнес. — 2007. — № 6. с. С. 82—89.
  26. Слюсар, В. (2005). Основные понятия теории и техники антенн. Антенные системы евклидовой геометрии. Фрактальные антенны. SMART-антенны. Цифровые антенные решетки (ЦАР). MIMO–системы на базе ЦАР.. Разделы 9.3—9.8 в книге «Широкополосные беспроводные сети передачи информации». / Вишневский В. М., Ляхов А. И., Портной С. Л., Шахнович И. В. — М.: Техносфера. — 2005. с. C. 498—569.
  27. Крупенин С. В. Фрактальные излучающие структуры и аналоговая модель фрактального импеданса. Дис. канд. физ.-мат. наук : 01.04.03, 01.04.04 / [Место защиты: Моск. гос. ун-т им. М. В. Ломоносова. Физ. фак.].- Москва, 2009.- 157 с.
  28. Бабичев Д. А. Разработка и исследование микрополосковой антенны на основе фрактального подхода. Дис. канд. техн. наук: - 05.12.07. [Место защиты: С.-Петерб. гос. электротехн. ун-т (ЛЭТИ)]. - Санкт-Петербург, 2016. - 104 с. Архівовано 19 червня 2018 у Wayback Machine.

Джерела інформації

Література
  • Фракталы в физике. Труды VI международного симпозиума по фракталам в физике. — М. : Мир, 1988. — 672 с.
  • Божокин С. В., Паршин Д. А. Фракталы и мультифракталы. — Ижевск : РХД, 2001. — 128 с.
  • Гринченко В. Т., Мацыпура В. Т., Снарский А. А. Введение в нелинейную динамику: Хаос и фракталы. — М. : URSS, 2010. — 280 с.
  • Гринченко В. Т., Мацыпура В. Т., Снарский А. А. Фракталы: от удивления к рабочему инструменту. — К. : Наукова думка, 2013. — 270 с.
  • Кроновер Р. М. Фракталы и хаос в динамических системах. — М. : Техносфера, 2006. — 488 с.
  • Ландэ Д. В. Фракталы и кластеры в информационном пространстве // Корпоративные системы. — 2005. — Вип. 6. — С. 35-39.
  • Мандельброт Б. Фрактальная геометрия природы. — Ижевск : ИКИ, 2010. — 656 с.
  • Мандельброт Б. Фракталы и хаос. — Ижевск : РХД, 2009. — 400 с.
  • Мандельброт Б. Фракталы, случай и финансы. — Ижевск : РХД, 2004. — 256 с.
  • Морозов А. Д. Введение в теорию фракталов. — Ижевск : ИКИ, 2002. — 160 с.
  • Пайтген Х.-О., Рихтер П. Х. Красота фракталов. — М. : Мир, 1993. — 176 с.
  • Федер Е. Фракталы. — М. : Мир, 1991. — 254 с.
  • Шредер М. Фракталы, хаос, степенные законы. — Ижевск : РХД, 2005. — 528 с.
  • Falconer K. Fractal Geometry: Mathematical Foundations and Applications. — Wiley, 2003.

Посилання
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.