Крива титрування
Крива́ титрува́ння — графічне відображення залежності визначуваної в ході титрування величини від об'єму доданого стандартного розчину (титранту). Побудова кривих проводиться в інструментальних методах аналітичної хімії, де відсутня можливість візуального визначення точки еквівалентності (наприклад, за індикатором).
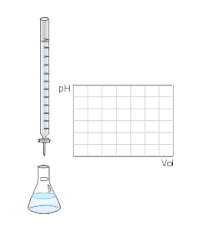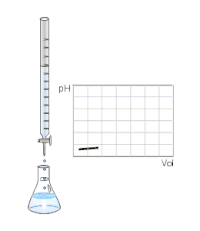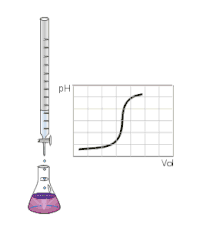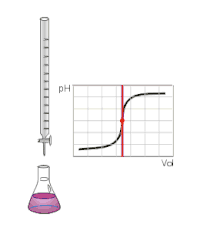
Побудова
Ординатою (віссю Y) у графіку залежності є параметр, що фіксується (pH, напруга, температура розчину тощо), а абсцисою (незалежною змінною, віссю X) — кількість доданого титранту. Інколи абсцисою виступає ступінь відтитрованості (позначається τ або f) — відношення кількості речовини титранту до кількості визначуваної речовини. Цей показник може використовуватися або у вигляді абсолютного значення, або у ж відсотках.
Якщо в ході титрування фіксовані значення змінюються на кілька порядків, для зручності застосовують побудову логарифмічних залежностей — величину A на осі Y представляють у вигляді -lg A (аналогічно до pH, який є логарифмом -lg H+). Логарифмічні криві характерні для кислотно-основних і окисно-відновних титрувань.
Обробка даних

Важливою властивістю кривої титрування є нерівномірність зміни визначуваної величини при в ході аналізу. Спочатку величина змінюється незначним чином, формуючи пологу частину кривої. По мірі наближення до точки еквівалентності зміни стають більш різкими (не рідкістю є моментальні, стрибкоподібні зміни), а після проходження точки вони зменшуються і формують другу пологу частину кривої (аналогічно можуть відбуватися другий, третій стрибки — у випадку титрування багатоосновних кислот). Саме на основі цих змін за допомогою математичної обробки здійснюється визначення точки еквівалентності — зазвичай її розраховують як:
- першу похідну від функції кривої — абсциса пікового значення відповідатиме об'єму доданого титранту;
- другу похідну від функції кривої — об'єм титранту є абсцисою у місці перетину похідною осі X (Y=0). Розрахунок за другою похідною надає точніші результати.
Джерела
- Harvey, D. Modern Analytical Chemistry. — 1st edition. — McGraw-Hill, 2000. — 798 p. — ISBN 0-07-237547-7. (англ.)
- Данцер К., Тан Э., Мольх Д. Аналитика. Систематический обзор / Под ред. Ю. А. Клячко. — М. : Химия, 1981. — С. 85—86. (рос.)
- Пискарёва С. К. и др. Аналитическая химия. — Издание 2-е. — М. : Высшая школа, 1994. — 384 с. — ISBN 5-06-002179-3. (рос.)
- Жаровський Ф. Г., Пилипенко А. Т., П'ятницький І. В. Аналітична хімія. — 2-е. — К. : Вища школа, 1982. — С. 392—393.