Логарифм

Логари́фм, або логари́тм,[1][2] (від грец. λόγος — «слово», і грец. ἀριθμός — «число») — число $x$ (показник степеня, степінь), яке показує, до якого степеня слід піднести число $a$ (основу), щоб одержати число $b$ .

\log _{a}b=x.

Графік функції log₂(x) проходить через точки з координатами (1, 0); (2, 1); (4, 2); (8, 3).
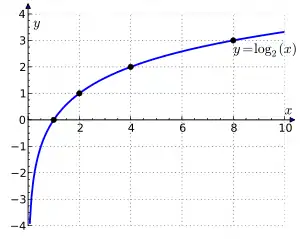
log₂(2) = 1, тому що 2¹ = 2,
log₂(4) = 2, тому що 2² = 4,
log₂(8) = 3, тому що 2³ = 8

Основна логаритмічна тотожність: $a^{x}=b$ або $a^{\log _{a}b}=b$ , де $a>0$ , $b>0$ та $a\neq 1$ .

Логаритми ввів Джон Непер на початку XVII століття як засіб спрощення розрахунків. Їх швидко почали застосовувати науковці та інженери для пришвидшення виконання обчислень із застосуванням логаритмічних лінійок і таблиць логаритмів. Логаритм дозволяє прискорити множення багатозначних чисел шляхом складання їхніх логаритмів. Наприклад, візьмімо два числа, які потрібно помножити: $42,5$ і $378$ . За допомогою таблиці логаритмів подивімося, що за основою $10$ ці числа мають логаритми (степені) $1,6284$ і $2,5775$ відповідно. Тобто, $42,5=10^{1,6284}$ i $378=10^{2,5775}$ . Таким чином, $42,5*378=10^{1,6284}*10^{2,5775}=10^{(1,6284+2,5775)}=10^{4,2059}$ . Виходить, що логаритмом добутку чисел $42,5$ і $378$ , за основою $10$ , є число $4,2059$ . З таблиці логаритмів легко знайти результат $\log _{10}{(42,5*378)}=4,2059$ .

Сучасне означення логаритмів увів Леонард Ейлер, який у XVIII столітті пов'язав їх з показниковою функцією.

Позначення

Позначення:

x=\log _{a}b

(логаритм числа

b

за основою

a

)

Існують особливі позначення для:

натуральних логаритмів (логаритмів за основою e):

\log _{e}a=\ln a

десяткових логаритмів (логаритмів за основою 10):

\log _{10}a=\lg a

двійкових логаритмів (логаритмів за основою 2):

\log _{2}a=\operatorname {lb} a

Логаритми були винайдені Джоном Непером на початку XVII століття як засіб для спрощення розрахунків і відтоді широко використовуються в науці, техніці. До винайдення комп'ютерів логаритмічна лінійка та таблиці логаритмів були повсякденним інструментом інженера.

Властивості

	Формула	Приклад
Добуток	$\log _{a}(xy)=\log _{a}x+\log _{a}y\,$	$\log _{3}243=\log _{3}(9\cdot 27)=\log _{3}9+\log _{3}27=2+3=5\,$
Частка	$\log _{a}\!\left({\frac {x}{y}}\right)=\log _{a}x-\log _{a}y\,$	$\lg \left({\frac {1}{1000}}\right)=\lg 1-\lg 1000=0-3=-3$
Степінь	$\log _{a}x^{p}=p\log _{a}x$	$\log _{2}64=\log _{2}2^{6}=6\log _{2}2=6\,$
Корінь	$\log _{a}{\sqrt[{p}]{x}}={\frac {1}{p}}\log _{a}x$	$\lg {\sqrt {1000}}={\frac {1}{2}}\lg 1000={\frac {3}{2}}=1{,}5$

Графіки логаритмічної функції за основами

\mathbb {} e

(червоний), 10 (зелений) та 1,7 (фіолетовий). Графік асимптотично наближається до осі y.

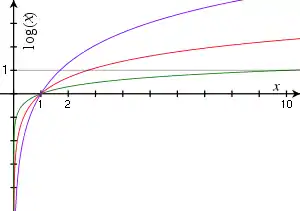
Ці властивості зробили логаритм надзвичайно корисною функцією. Додавання та віднімання набагато простіші операції ніж множення та ділення, й, маючи таблицю логаритмів, можна сильно спростити складні обчислення.

Формула:

\log _{a}x={\frac {\log _{b}x}{\log _{b}a}}

дозволяє переходити від одної основи до іншої.

Інші тотожності:

$a^{log_{a}b}=b$
$a^{log_{c}b}=b^{log_{c}a}$
$\log _{b^{c}}a={\tfrac {1}{c}}\log _{b}a$
$\log _{a}b={\frac {1}{\log _{b}a}}$

Логаритмічна функція

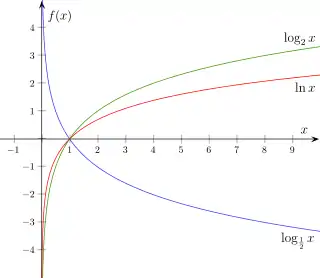
Логаритмічна функція $\,\!y=\log _{b}x$ ставить у відповідність кожному значенню змінної її логаритм за наперед обраною основою $\,\!b$ .

Властивості логаритмічної функції:

множина визначення логаритмічної функції $D=(0,+\infty )$ ,
логаритмічна функція є монотонною, причому
- є зростаючою якщо $\,\!b>1$
- є спадною якщо $\,\!0<b<1$
логаритмічні функції за різними основами є пропорційними,
функція $\ y=\log _{b}x$ є оберненою до показникової функції $\ x=b^{y}$ ,
похідна логаритмічної функції:

{\frac {d\ln x}{dx}}={\frac {1}{x}},\qquad {\frac {d\log _{b}x}{dx}}={\frac {1}{x\ln b}}

первісна логаритмічної функції:

\int \ln x\,dx=x(\ln x-1)+C

(див. також таблицю інтегралів логаритмічних функцій)

похідна від логаритму функції називається логаритмічною похідною

{\frac {d}{dx}}\ln(f(x))={\frac {f'(x)}{f(x)}}.

спеціальна функція інтегральний логаритм:

{\rm {li}}(x)=\int _{0}^{x}{\frac {dt}{\ln t}},\quad x\neq 1

розклад у ряд Тейлора

\ln(1+x)=\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}x^{n}=x-{\frac {x^{2}}{2}}+{\frac {x^{3}}{3}}-\cdots

стала Ейлера—Маскероні

\gamma =\lim _{n\rightarrow \infty }\left[\left(\sum _{k=1}^{n}{\frac {1}{k}}\right)-\ln(n)\right]

Натуральні логаритми

Зв'язок з десятковим логаритмом: $\ln x\approx 2{,}30259\ \lg x;\ \ \lg x\approx 0{,}43429\ \ln x$ .

Як зазначено вище, для похідної натурального логаритму справедлива проста формула:

(\ln x)'={\frac {1}{x}}

З цієї причини у математичних дослідженнях дуже часто використовують саме натуральні логаритми. Вони часто з'являються при розв'язку диференціальних рівнянь, дослідженні статистичних закономірностей (наприклад, розподіл простих чисел) тощо.

Невизначений інтеграл від натурального логаритму легко знайти інтегруванням за частинами:

\int {\ln x\,\mathrm {d} x}=x\ln x-x+C

Розклад у ряд Тейлора може бути представлений наступним чином:
при $-1<x\leqslant 1$ наступна рівність є справедливою

\ln(1+x)=x-{\frac {x^{2}}{2}}+{\frac {x^{3}}{3}}-{\frac {x^{4}}{4}}+\dots

(1)

Зокрема,

\ln 2=1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+\dots

Формула (1) не має великої практичної цінності через те, що ряд дуже повільно сходиться і значення $x$ є обмеженим у доволі вузькому діапазоні. Однак, не складно отримати з неї зручнішу формулу:

\ln \left({\frac {1+x}{1-x}}\right)=2\left(x+{\frac {x^{3}}{3}}+{\frac {x^{5}}{5}}+{\frac {x^{7}}{7}}+\dots \right)

(2)

Цей ряд сходиться швидше, а крім цього, ліва частина формули тепер може виразити логаритм будь-якого додатного числа.

Двійкові логаритми

Логаритми за основою 2 широко застосовуються в теорії інформації. Двійковий логаритм натурального числа $N$ дозволяє визначити число цифр $b(N)$ у внутрішньому комп'ютерному (бітовому) поданні цього числа:

B(N)=\lfloor \operatorname {lb} N\rfloor +1

(дужки позначають цілу частину числа).

Інформаційна ентропія — міра кількості інформації, також заснована на двійкових логаритмах.

Оцінка асимптотичної складності рекурсивних алгоритмів, заснованих на принципі «розділяй та володарюй» — таких, як швидке сортування, швидке перетворення Фур'є, двійковий пошук виконується з використанням двійкових логаритмів.

У теорії музики, щоб вирішити питання про те, на скільки частин ділити октаву, потрібно відшукати раціональне наближення для $\log _{2}{\frac {3}{2}}\approx 0{,}585.$ Якщо розкласти це число в безперервний дріб, то третій дріб, що підходить, (7/12) дозволяє обґрунтувати класичний розподіл октави на 12 півтонів.

Десяткові логаритми

Рисунок 2а. Логаритмічна шкала.

Рисунок. 2б. Логаритмічна шкала з позначеннями.

Логаритми за основою 10 (позначаються як $lg a$ ) до винайдення калькуляторів широко використовувалися для обчислень. Нерівномірна шкала десяткових логаритмів зазвичай наноситься і на логаритмічні лінійки. Подібна шкала використовується у багатьох областях науки, наприклад:

Фізика — інтенсивність звуку (децибели).
Астрономія — шкала яскравості зірок.
Хімія — активність водневих іонів (pH).
Сейсмологія — шкала Ріхтера.
Теорія музики — нотна шкала, по відношенню до частот нотних звуків.
Історія — логаритмічна шкала часу.

Логаритмічна шкала також широко використовується для виявлення показника степеня у показникових залежностях і коефіцієнта у показнику експоненти. При цьому графік, побудований у логаритмічному масштабі по одній або двох осях, приймає вигляд прямої, яка є простішою для дослідження.

Логаритмічна функція комплексної змінної

Визначення і властивості

Для комплексних чисел логаритм визначається так само як і для дійсних. На практиці використовується майже завжди натуральний комплексний логаритм, який позначимо як $\mathrm {Ln} \,w$ і визначимо як множину всіх комплексних чисел $z$ таких, що $e^{z}=w$ . Комплексний логаритм існує для будь-якого $w\neq 0$ , і його дійсна частина визначається однозначно, тоді як уявна частина має нескінченну множину значень. З цієї причини його називають багатозначною функцією. Якщо представити $w$ у показниковій формі:

w=r\cdot e^{i\varphi }

,

то логаритм $\mathrm {Ln} \,w$ знаходиться за формулою:

\mathrm {Ln} \,w=\{\ln r+i\left(\varphi +2\pi k\right),\,k\in \mathbb {Z} \}.

Тут $\ln \,r$ — дійсний логаритм, $r=|w|$ , $k$ — довільне ціле число. Значення, що отримуємо при $k=0$ , називається головним значенням комплексного натурального логаритму; прийнято брати значенням аргументу у ньому $\varphi$ в інтервалі $(-\pi ,\pi ]$ . Відповідна (вже однозначна) функція називається головною гілкою логаритму і позначається $\ln \,z$ . Інколи через $\ln \,z$ також позначають значення логаритму, що лежить не на головній гілці.

З формули маємо наступні наслідки:

Дійсна частина логаритму визначається за формулою:

\operatorname {Re} (\ln(x+iy))={\frac {1}{2}}\ln(x^{2}+y^{2})

Логаритм від'ємного числа знаходиться за формулою:

\ln(-x)=\ln x+i\pi (2k+1)\qquad (x>0,\ k=0,\pm 1,\pm 2\dots )

Оскільки комплексні тригонометричні функції пов'язані з експонентою (формула Ейлера), то комплексний логаритм як функція, що обернена до експоненти, пов'язаний з оберненими тригонометричними функціями. Приклад такого зв'язку:

\arcsin z=-i\ln(iz+{\sqrt {1-z^{2}}})

Приклади

Наведемо головне значення логаритму для деяких аргументів:

$~\ln(-1)=i\pi$
$\ln(i)=i{\frac {\pi }{2}}$
$\ln(-i)=-i{\frac {\pi }{2}}$

Потрібно бути обережним при перетвореннях комплексних логаритмів, беручи до уваги, що вони багатозначні, тому з рівності логаритмів будь-яких виразів не виходить рівність цих виразів. Приклад помилкових міркувань:

i\pi =\ln(-1)=\ln((-i)^{2})=2\ln(-i)=2(-i\pi /2)=-i\pi

— неправильно (суперечність).

Відзначимо, що зліва стоїть головне значення логаритма, а справа — значення з нижчої гілки ( $k=-1$ ). Причина помилки — неправильне використання властивості $\log _{a}{(b^{p})}=p~\log _{a}b$ , яка, загалом, справджується у випадку комплексних чисел для всього нескінченного набору значень логаритма, а не тільки для головного значення.

Аналітичне продовження

Рисунок 3. Ріманова поверхня, на якій задається функція

{\text{Ln}}\;z

.

Логаритм комплексного числа також може бути визначений як аналітичне продовження дійсного логаритму на всю комплексну площину. Нехай крива $\Gamma$ починається в одиниці, не проходить через нуль і не перетинає від'ємну частину дійсної осі. Тоді головне значення логаритму в кінцевій точці $w$ кривої $\Gamma$ можна визначити за формулою:

\ln w=\int \limits _{\Gamma }{dz \over z}

Якщо $\Gamma$ — проста крива (без самоперетину), то для чисел, що лежать на ній, логаритмічні тотожності можна застосовувати без обмежень, наприклад

\ln(wz)=\ln w+\ln z,~\forall z,w\in \Gamma \colon zw\in \Gamma

Якщо дозволити кривій $\Gamma$ перетинати від'ємну частину дійсної осі, то перший такий перетин переносить результат з гілки головного значення на сусідню гілку, а кожен наступний перетин викликає аналогічне зміщення по гілках логаритмічної функції (дивіться рисунок).

Із формули аналітичного продовження виходить, що на будь-якій гілці логаритму

\ln 'z={1 \over z}

Для будь-якого околу $S$ , що містить точку $0$ :

\oint \limits _{S}{dz \over z}=2\pi i

Інтеграл береться у додатному напрямку (проти годинникової стрілки). Ця тотожність лежить в основі теорії лишків.

Можна також визначити аналітичне продовження комплексного логаритма за допомогою ряду, що наведений вище (1), і який узагальнений для випадку комплексного аргументу. Однак із вигляду розкладу в ряд маємо наслідок, що він дорівнює нулю в одиниці, тобто ряд відноситься лише до головної гілки багатозначної функції комплексного логаритма.

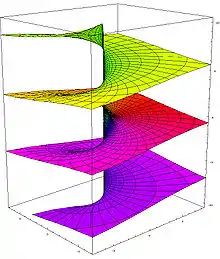
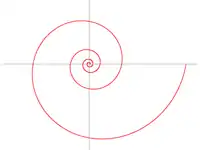
Поверхня Рімана

Комплексна логаритмічна функція — приклад поверхні Рімана; її уявна частина (рисунок 3) складається з нескінченного числа гілок, що закручені у вигляді спіралі. Ця поверхня однозв'язна; єдиний її нуль (першого порядку) отримуємо при $z=1$ , особливі точки: $z=0$ і $z=\infty$ (точки розгалуження нескінченного порядку).

Ріманова поверхня логаритму є універсальним накриттям для комплексної площини без точки $0$ .

Історія

Ще у VIII столітті індійський математик Вірасена розвинув концепцію ардхакчеди, що означала скільки разів число виду 2ⁿ можна поділити на два. Для чисел, які не є цілими степенями двійки ардхакчеда залишалася невизначеною. Він описав також трікачеду та чатуртхачеду — відповідні числа для основ 3 і 4[3][4]. 1544 року Михаель Штифель опублікував у Нюрнбергу книгу Arithmetica integra з таблицею[5] цілих чисел і степенів двійки, які їм відповідають[6][7]. Ці ранні дослідження можна вважати попередниками логаритмів.

Джон Непер (1550—1617)

Метод логаритмування був опублікований Джоном Непером у 1614 році в книзі під назвою Mirifici Logarithmorum Canonis Descriptio (Опис чудового правила логарифмів)[8]. Незалежно від Непера логаритми відкрив Юст Бурґі, але його публікація з'явилася на 6 років пізніше[9].

Непер не тільки сформулював правило множення чисел з використанням логаритмів, а й побудував перші логаритмічні таблиці. Методом повторного віднімання Непер обрахував 10⁷(1 − 10⁻⁷)^L для L від 1 до 100. Для L=100 результат приблизно дорівнює 0.99999 = 1 − 10⁻⁵. Далі він порахував добутки цих чисел при множенні на 10⁷(1 − 10⁻⁵)^L для L від 1 до 50, і, аналогічно, добутки цих чисел при множенні на 0.9995 ≈ (1 − 10⁻⁵)²⁰ й 0.99 ≈ 0.995²⁰. Обчислення тривали 20 років. Як наслідок він отримав число L, яке є розв'язком рівняння

N=10^{7}{(1-10^{-7})}^{L}.\,

для чисел від 5 до 10 000 000.

Спочатку Непер назвав L штучним числом, але потім запровадив новий термін — логаритм. У сучасній нотації з використанням натуральних логаритмів це співвідношення має вигляд[10]

L=\log _{(1-10^{-7})}\!\left({\frac {N}{10^{7}}}\right)\approx 10^{7}\log _{\frac {1}{e}}\!\left({\frac {N}{10^{7}}}\right)=-10^{7}\log _{e}\!\left({\frac {N}{10^{7}}}\right),

де наближення відповідає тому, що

{(1-10^{-7})}^{10^{7}}\approx {\frac {1}{e}}.\,

з дуже малою похибкою.

Дуже швидко винахід Непера здобув широке визнання. Роботи італійця Бонавентури Кавальєрі та німця Йоганна Кеплера розвинули і вдосконалили концепцію[11]. 1620 року Едмунд Вінґейт збудував першу логаритмічну лінійку.

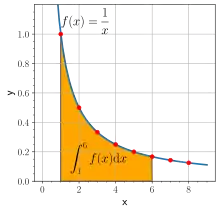
Гіпербола y = 1/x (червона крива) і площа від x = 1 to 6 (помаранчева).

1647 року Грегуар де Сент-Вінсент отримав зв'язок між логаритмом та квадратурою гіперболи, зауваживши, що площі під графіком функції y = 1/x між 1 та числами a та b задовольняють співвідношенню:

S(ab)=S(a)+S(b)

.

Натуральні логаритми були вперше описані Нікола Меркаром у праці Logarithmotechnia 1668 року[12], хоча ще у 1619 вчитель математики Джон Спейделл складав таблицю натуральних логарифмів[13].

Приблизно 1730 року Леонард Ейлер дав означення експоненти та натурального логаритма як

e^{x}=\lim _{n\rightarrow \infty }(1+x/n)^{n},

\ln(x)=\lim _{n\rightarrow \infty }n(x^{1/n}-1).

Ейлер показав, що ці функції обернені одна одній[14][15][16].

Деякі практичні застосування

Логаритмічна лінійка

Типова логаритмічна лінійка. Показано обчислення добутку 1,3 × 2 = 2,6

Кругла логаритмічна лінійка.

Логаритмі́чна лінійка — аналоговий обчислювальний пристрій, що дозволяє виконувати кілька математичних операцій, основними з яких є множення і ділення чисел.

Найпростіша логаритмічна лінійка складається з двох шкал у логаритмічному масштабі, що здатні пересуватися одна відносно одної. Складніші лінійки містять додаткові шкали і прозорий повзунок з кількома поділками. На зворотній стороні лінійки можуть знаходитися різні довідкові матеріали.

За допомогою додаткових шкал можна здійснювати піднесення до степеня (частіше всього до квадрата і куба), обчислення логаритмів, тригонометричних функцій та обернених операцій (добування квадратних і кубічних коренів, обчислення експоненти та обернених тригонометричних функцій), перетворення величин між різними системами (наприклад, кіловатів на кінські сили чи навпаки) та деякі інші операції.

Принцип дії

Основний принцип дії логаритмічної лінійки заснований на тому, що множення і ділення чисел замінюється відповідно додаванням і відніманням їх логарифмів:

lg (xy) = lg x + lg y

,

lg (x / y) = lg x - lg y

.

Для того щоб обчислити добуток двох чисел, початок (чи кінець) рухомої шкали суміщують із першим множником на нерухомій шкалі, а на рухомій шкалі відшукують другий множник. Напроти нього на нерухомій шкалі знаходиться результат множення чисел.

Щоб розділити числа, на рухомій шкалі знаходять дільник і суміщують його з діленим на нерухомій шкалі. Початок (або кінець) рухомої шкали вказує на результат.

За допомогою логаритмічної лінійки знаходять лише мантису числа, його порядок обчислюється усно. Точність обчислення звичайних логаритмічних лінійок — два-три десяткових знаки. Для виконання інших операцій застосовують повзунок та додаткові шкали. Слід відзначити, що, незважаючи на простоту, на логаритмічній лінійці можна виконувати досить складні розрахунки.

Історія

Перший варіант лінійки розробив англійський математик-аматор Вільям Отред 1622 року.

Раніше випускалися посібники з їх використання досить великого обсягу[17][18].

В СРСР логаритмічні лінійки широко застосовувалися для виконання інженерних розрахунків приблизно до початку 80-х років XX століття, коли їх було витіснено калькуляторами.

Годинник Breitling Navitimer

Відродження логаритмічної лінійки відбулося на початку XXI сторіччя внаслідок попиту на наручні годинники та хронометри із вбудованим простим обчислювальним пристроєм. Його виконано у вигляді двох логаритмічних шкал навколо циферблату годинника, одна з яких може обертатися (базель). За примхою виробників такі пристрої зазвичай називають «навігаційна лінійка». За допомогою такого пристрою можна виконувати переведення миль на кілометри, літрів на галони, метри за секунду в кілометри за годину тощо[19]. На відміну від калькулятора одразу будується таблиця відповідності величин.

Прикладом таких годинників можна вважати Breitling Navitimer, CITIZEN (моделі BJ7010-59E, JQ8005-56E, JR3130-55E), Orient (моделі OCEM58002DV, OCTD09001B, OCTD09003D) та деякі інші.

Логаритмічна спіраль

Побудова логаритмічної спіралі. Анімація.

Логаритмічна спіраль (нахил 10°).

Логаритмічна спіраль або ізогональна спіраль — особливий вид спіралі, що часто зустрічається в природі. Логаритмічна спіраль була вперше описана Декартом і пізніше інтенсивно досліджена Бернуллі, який називав її Spira mirabilis — «дивовижна спіраль». Власне термін «логаритмічна спіраль» (фр. spirale logarithmique) першим вжив П'єр Варіньон[20]

Рівняння

У полярних координатах рівняння кривої може бути записано як

r=ae^{b\theta }\,

або

\vartheta ={\frac {1}{b}}\ln(r/a),

що пояснює назву «логаритмічна».

У параметричній формі його може бути записано як

x(t)=r\cos t=ae^{bt}\cos t\,,

y(t)=r\sin t=ae^{bt}\sin t\,,

де a, b — дійсні числа.

Властивості

Кут, що утворюється дотичною в довільній точці логаритмічної спіралі з радіус-вектором точки дотику, постійний і залежить лише від параметра $b.$ $\text{[math]}$
- У термінах диференціальної геометрії це може бути записано як
  ${\frac {\langle \mathbf {r} (\theta ),\mathbf {r} '(\theta )\rangle }{\|\mathbf {r} (\theta )\|\|\mathbf {r} '(\theta )\|}}={\frac {b}{\sqrt {1+b^{2}}}}=\cos \varphi .$
Похідна функції $\mathbf {r} '(\vartheta )$ пропорційна параметру b. Іншими словами, він визначає, наскільки щільно і в якому напрямку закручується спіраль. У граничному випадку, коли $b=0\;(\varphi =\pi /2)$ спіраль вироджується в коло радіусу a. Навпаки, коли b прямує до нескінченності $(\varphi \rightarrow 0),$ спіраль наближається до прямої лінії. Кут, що доповнює $\varphi$ до 90 °, називають нахилом спіралі.
Розмір витків логаритмічної спіралі поступово збільшується, але їх форма залишається незмінною. Можливо, внаслідок цієї властивості, логаритмічна спіраль з'являється в багатьох зростаючих формах, подібних до мушлель молюсків і квіток соняшників.

Мушля молюска Наутілуса за формою близька до логаритмічної спіралі
Область низького тиску над Ісландією
Спіральна галактика «Вир»
Секція множини Мандельброта, що є логаритмічною спіраллю

Примітки

Revue statistique de l'Ukraine (українською). 1928.
Fizychniĭ zbirnyk (рос.). Vyd-vo Lʹvivsʹkoho derz︠h︡. universytetu. 1959.
Gupta, R. C. (2000). History of Mathematics in India. У Hoiberg, Dale; Ramchandani. Students' Britannica India: Select essays. New Delhi: Popular Prakashan. с. 329.
Dr. Hiralal Jain, ред. (1996). THE SHATKHANDAGAMA OF PUSHPADANTA AND BHOOTABAL (вид. 3rd). Solapur: Jain Samskriti Samrakshaka Sangha. Архів оригіналу за 11 травня 2011. Процитовано 22 червня 2011. Проігноровано невідомий параметр |unused_data= (довідка), part 3-4-5, book 4
Stifelio, Michaele (1544). Arithmetica Integra. London: Iohan Petreium.
Bukhshtab, A.A.; Pechaev, V.I. (2001). Arithmetic. У Hazewinkel, Michiel. Encyclopedia of Mathematics. Springer. ISBN 978-1-55608-010-4.
Vivian Shaw Groza and Susanne M. Shelley (1972). Precalculus mathematics. New York: Holt, Rinehart and Winston. с. 182. ISBN 978-0-03-077670-0.
Ernest William Hobson (1914). John Napier and the invention of logarithms, 1614. Cambridge: The University Press.
Boyer 1991, Chapter 14, section "Jobst Bürgi"
William Harrison De Puy (1893). The Encyclopædia Britannica: a dictionary of arts, sciences, and general literature ; the R.S. Peale reprint, 17 (вид. 9th). Werner Co. с. 179.
Maor, Eli (2009). E: The Story of a Number. Princeton University Press. ISBN 978-0-691-14134-3., section 2
J. J. O'Connor; E. F. Robertson (2001-09). The number e. The MacTutor History of Mathematics archive. Процитовано 02/02/2009.
Cajori, Florian (1991). A History of Mathematics (вид. 5th). Providence, RI: AMS Bookstore. ISBN 978-0-8218-2102-2., p. 152
Maor, Eli (2009). e: The Story of a Number. Princeton University Press. ISBN 978-0-691-14134-3., sections 1, 13
Eves, Howard Whitley (1992). An introduction to the history of mathematics. The Saunders series (вид. 6th). Philadelphia: Saunders. ISBN 978-0-03-029558-4., section 9-3
Boyer, Carl B. (1991). A History of Mathematics. New York: John Wiley & Sons. ISBN 978-0-471-54397-8., p. 484, 489
Панов Д.Ю. Счетная линейка. — 21-е изд. — М : Наука, 1973. — 168 с.(рос.)
Богомолов Н.В. Практические занятия с логарифмической линейкой (сборник задач). — М : Высшая школа, 1977. — 103 с.(рос.)
Citizen BJ7010-59E. Watch Zone. Архів оригіналу за 30 червня 2013. Процитовано 2 листопада 2010.
Spirale logarithmique. (фр.)

Див. також

Література

Сторчай, Володимир Федорович. Показникові і логарифмічні рівняння: навч. посібник / В. Ф. Сторчай ; Дніпропетровський держ. ун-т. — К. : [б.в.], 1995. — 100 с
Щербинин, Гарий Петрович. Показательно- логарифмические выражения, уравнения и неравенства: учеб. пособие / Г. П. Щербинин, Т. А. Недзельская ; ИСИО, Харьковский гос. технический ун-т радиоэлектроники. — Х. : [б.в.], 1995. — 60 с.
Барановська, Галина Григорівна. Практикум з математики: Показникова та логарифмічна функції: навч. посібник для вступників до вузів / Г. Г. Барановська, В. В. Ясінський ; Національний технічний ун-т України «Київський політехнічний ін-т». Факультет довузівської підготовки. — К. : [б.в.], 1998. — 124 с.
Кушнір, Ісаак. У світі логарифмів. — К. : Факт, 2004. — 136 с.: рис.

Посилання

Функція логарифмічна // Універсальний словник-енциклопедія. — 4-те вид. — К. : Тека, 2006.

Логарифмічна функція // Вища математика в прикладах і задачах / Клепко В.Ю., Голець В.Л.. — 2-ге видання. — К. : Центр учбової літератури, 2009. — С. 179. — 594 с.
Динамічні математичні моделі FIZMA.neT

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Revue statistique de l'Ukraine (українською). 1928.

[2] Fizychniĭ zbirnyk (рос.). Vyd-vo Lʹvivsʹkoho derz︠h︡. universytetu. 1959.

[3] Gupta, R. C. (2000). History of Mathematics in India. У Hoiberg, Dale; Ramchandani. Students' Britannica India: Select essays. New Delhi: Popular Prakashan. с. 329.

[4] Dr. Hiralal Jain, ред. (1996). THE SHATKHANDAGAMA OF PUSHPADANTA AND BHOOTABAL (вид. 3rd). Solapur: Jain Samskriti Samrakshaka Sangha. Архів оригіналу за 11 травня 2011. Процитовано 22 червня 2011. Проігноровано невідомий параметр |unused_data= (довідка), part 3-4-5, book 4

[5] Stifelio, Michaele (1544). Arithmetica Integra. London: Iohan Petreium.

[6] Bukhshtab, A.A.; Pechaev, V.I. (2001). Arithmetic. У Hazewinkel, Michiel. Encyclopedia of Mathematics. Springer. ISBN 978-1-55608-010-4.

[7] Vivian Shaw Groza and Susanne M. Shelley (1972). Precalculus mathematics. New York: Holt, Rinehart and Winston. с. 182. ISBN 978-0-03-077670-0.

[8] Ernest William Hobson (1914). John Napier and the invention of logarithms, 1614. Cambridge: The University Press.

[9] Boyer 1991, Chapter 14, section "Jobst Bürgi"

[10] William Harrison De Puy (1893). The Encyclopædia Britannica: a dictionary of arts, sciences, and general literature ; the R.S. Peale reprint, 17 (вид. 9th). Werner Co. с. 179.

[11] Maor, Eli (2009). E: The Story of a Number. Princeton University Press. ISBN 978-0-691-14134-3., section 2

[12] J. J. O'Connor; E. F. Robertson (2001-09). The number e. The MacTutor History of Mathematics archive. Процитовано 02/02/2009.

[13] Cajori, Florian (1991). A History of Mathematics (вид. 5th). Providence, RI: AMS Bookstore. ISBN 978-0-8218-2102-2., p. 152

[14] Maor, Eli (2009). e: The Story of a Number. Princeton University Press. ISBN 978-0-691-14134-3., sections 1, 13

[15] Eves, Howard Whitley (1992). An introduction to the history of mathematics. The Saunders series (вид. 6th). Philadelphia: Saunders. ISBN 978-0-03-029558-4., section 9-3

[16] Boyer, Carl B. (1991). A History of Mathematics. New York: John Wiley & Sons. ISBN 978-0-471-54397-8., p. 484, 489

[17] Панов Д.Ю. Счетная линейка. — 21-е изд. — М : Наука, 1973. — 168 с.(рос.)

[18] Богомолов Н.В. Практические занятия с логарифмической линейкой (сборник задач). — М : Высшая школа, 1977. — 103 с.(рос.)

[19] Citizen BJ7010-59E. Watch Zone. Архів оригіналу за 30 червня 2013. Процитовано 2 листопада 2010.

[20] Spirale logarithmique. (фр.)