Кістякове дерево

Кістякове дерево (англ. Spanning tree) зв'язаного неорієнтованого графу — ациклічний (тобто, не має циклів) зв'язний підграф цього графу, який містить всі його вершини[1]. Неформально кажучи, кістякове дерево складається з деякої підмножини ребер графу, таких, що рухаючись цими ребрами можна з будь-якої вершини графу потрапити до будь-якої іншої.
Кістякове дерево також називають каркасним деревом[1], покриваючим деревом[джерело?], кістяком або каркасом графу[2].

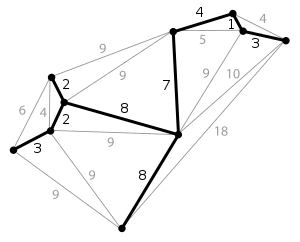
Граф з мінімальним каркасним деревом.

Властивості

Будь-яке каркасне дерево у графі з n вершинами містить рівно n — 1 ребер. Кількість кістякових дерев у повному графі з n вершинами подається відомою формулою Келі:

У загальному випадку, кількість кістякових дерев у довільному графі може бути обчислено за допомогою так званої матричної теореми про дерева[джерело?].

Каркасне дерево може бути побудовано майже будь-яким алгоритмом обходу графу, наприклад пошуком у глибину або у ширину. Воно складається з усіх пар ребер (u, v), таких, що алгоритм, переглядаючи вершину u виявляє в її списку суміжності нову, невиявлену раніше вершину v. Кістякове дерево, побудоване обходом графу починаючи з вершини s за алгоритмом Дейкстри, має властивість, що найкоротший шлях у графі з вершини s до будь-якої іншої вершини — це шлях з s до цієї вершини в побудованому дереві.

Існує кілька паралельних і розподілених алгоритмів пошуку каркасного дерева. Як практичний приклад розподіленого алгоритму можна навести протокол STP.

Якщо кожному ребру графу присвоєно вагу, то пошук оптимального каркасного дерева, яке мінімізує суму ваги його ребер здійснюють численні алгоритми пошуку мінімального каркасного дерева.

Задача про пошук кістяка, в якому степінь кожної вершини не перевищує деякої наперед заданої константи k, є NP-повною.

Узагальнення

Поняття кістяковий ліс неоднозначне, під ним можуть розуміти один з наступних підграфів:

  • Будь-який ациклічний підграф, до якого входять всі вершини графу, але він не є зв'язним[джерело?];
  • У незв'язному графі — підграф, що складається з об'єднання каркасних дерев для кожної його компоненти зв'язності[1].

Див. також

Посилання
  1. Р.М. Трохимчук. Теорія графів. — Навчальний посібник для студентів факультету кібернетики. — К : РВЦ «Київський університет», 1998. — С. 24. — ISBN 966-594-043-0.
  2. Ю. Нікольский, В. Пасічник, Ю. Щербина. Дискретна математика. — К : BHV, 2007. — С. 368. — ISBN 978-966-552-201-0.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.