Мінімальне кістякове дерево
Мінімальне кістякове дерево у зв'язаному, зваженому, неорієнтованому графі — це кістяк цього графу, що має мінімальну можливу вагу, де під вагою дерева розуміється сума ваг його ребер.
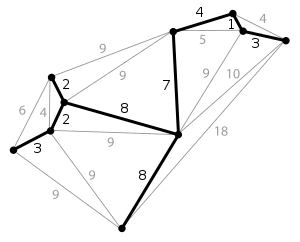
Приклад мінімального кістякового дерева в планарному графі. Кожне ребро має позначку з вагою, яка приблизно пропорційно його довжині.
Визначення
Нехай маємо граф де це множина вершин, а це множина ребер. І для кожного ребра відома його вага Мінімальним кістяковим деревом називається множина що поєднує всі вершини і чия повна вага
є найменшою.[1]
Алгоритми знаходження МКД
Існує декілька алгоритмів для знаходження мінімального кістякового дерева. Деякі найвідоміші з них перераховані нижче:
Див. також
Примітки
- Томас Кормен; Чарльз Лейзерсон, Рональд Рівест, Кліфорд Стайн (2009) [1990]. 23 Minimum spanning tree. Вступ до алгоритмів (вид. 3rd). MIT Press і McGraw-Hill. с. 624. ISBN 0-262-03384-4.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.
