Малокутове наближення
Малокутове наближення або апроксимація малих кутів це корисне спрощення базових тригонометричних функцій, яке буде досить точним при ліміті коли кут. Вони є усіченим рядом Тейлора для базових тригонометричних функцій за допомогою властивостей наближення другого порядку. [1] Таке спрощення дає наступну формулу:
- ,
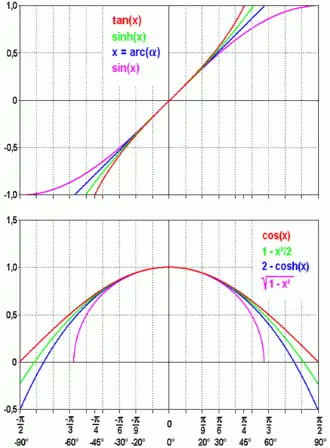
де θ це кут в радіанах.
Апроксимація малих кутів корисна в багатьох застосуваннях фізики, включаючи механіку, електромагнетизм, оптику (де воно є основою паралаксіальної оптики), картографії, астрономії, та ін.
Обґрунтування
Графічне
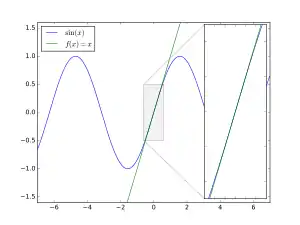
Точність наближення наглядно видно нижче на графіках 1 і 2. З тим як кут наближається до нуля, очевидно, що різниця між апроксимованою прямою і справжньою функцією значно зменшується.
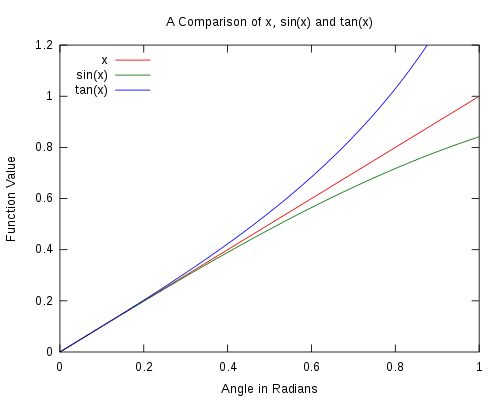 Графік 1. Порівняння базової парної тригонометричної функції із значенням кута θ. Видно, що при зменшенні значення кута до 0 наближення стає кращим.
Графік 1. Порівняння базової парної тригонометричної функції із значенням кута θ. Видно, що при зменшенні значення кута до 0 наближення стає кращим.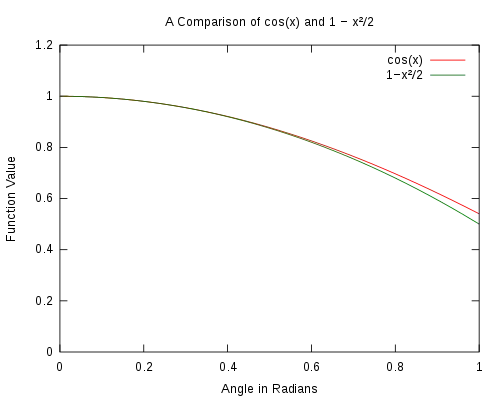 Графік 2. Порівняння функції cos(θ) з 1 - θ2/2. Видно, що при зменшенні значення кута до 0 наближення стає кращим.
Графік 2. Порівняння функції cos(θ) з 1 - θ2/2. Видно, що при зменшенні значення кута до 0 наближення стає кращим.
Геометричне
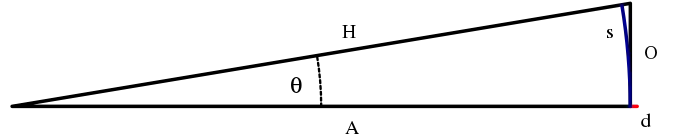
В червоній частині справа, d, є різницею між довжиною гіпотенузи, H, і прилеглої сторони, A. Як видно, H і A мають приблизно однакову довжину, що означає що cos θ близький до 1 і дозволяє відкинути червону різницю.
Протилежна вертикальна сторона, O, приблизно дорівнює довжині синьої дуги, s. Узагальнюючи факти з геометрії, s = A*θ, із тригонометрії, sin θ = O/H і tan θ = O/A, а із зображення беремо що, і , що приводить до:
- .
Спростивши, отримаємо,
- .
Алгебраїчне
Розширенням Маклорена (розкладання в ряд Тейлора при наближенні до 0) відповідної тригонометричної функції є [1]
де θ це кут в радіанах. У більш простому вигляді,
Легко побачити що другий найзначиміший (viz., третього порядку) терм зменшується в кубічній пропорції відносно першого терму; тому, навіть для такого не дуже малого значення як 0.01, значення другого значимого терму буде мати порядок 0.000001, або одну десятитисячну від першого терма. Таким чином, можна сміливо апроксимувати:
В подальшому, оскільки значення косинуса малого кута дуже близький одиниці, а тангенс задається як відношення синуса до косинуса, маємо
- .
Похибка апроксимації

Малюнок 3 показує похибку апроксимації малих кутів. Кути, при яких відносна похибка перевищує 1% є наступними:
- tan θ ≈ θ при приблизно 0.176 радіанах(10°).
- sin θ ≈ θ при приблизно 0.244 радіан (14°).
- cos θ ≈ 1 - θ2/2 при приблизно 0.664 радіан (38°).
Приклади застосування
Астрономія
В астрономії, зображення, яке займає образ віддаленого об'єкта зазвичай має розмір лише в декілька арксекунд, тому в даному випадку досить добре застосовується малокутове наближення. Зв'язок лінійного розміру (D) із кутовим розміром (X) і дистанцією від спостерігача (d) задається простою формулою
- D = X · d / 206,265
де X вимірюється в арксекундах.
Число 206,265 приблизно дорівнює кількості арксекунд в одному колі (1,296,000), розділене на 2π.
Точна формула має наступний вигляд:
- D = d tan(X·2π/1,296,000)
а вищезгадане спрощення випливає із заміни tan(X) на X.
Примітки
- Boas, Mary L. (2006). Mathematical Methods in the Physical Sciences. p. 26: Wiley. с. 839. ISBN 978-0-471-19826-0.