Радіан
Радіа́н (у математиці та фізиці) — це одиниця вимірювання площинних кутів в Міжнародній системі одиниць SІ.
| Радіан | ||||
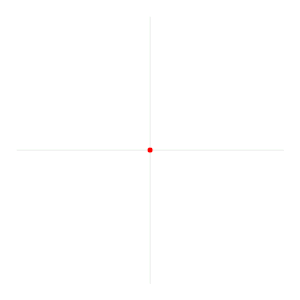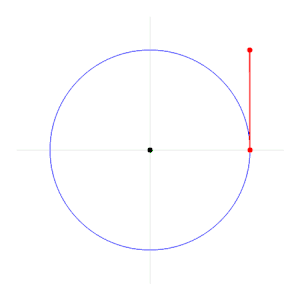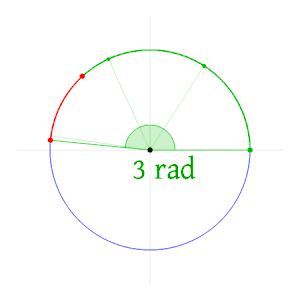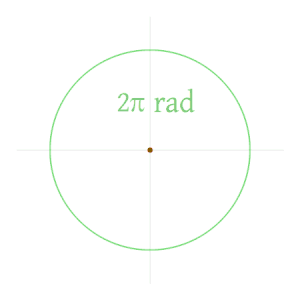 | ||||
| Кут 1 радіан відтинає дугу, довжина якої дорівнює радіусу кола | ||||
| Загальна інформація | ||||
|---|---|---|---|---|
| Система одиниць | Похідні одиниці SI | |||
| Одиниця | кута | |||
| Символ | рад або rad | |||
| Розмірність | безрозмірнісна, як відношення довжини дуги до радіуса 1 мм | |||
| Перерахунок в інші системи | ||||
| 1 рад в... | дорівнює... | |||
| мілірадіанах | 1000 мрад | |||
| обертах | 12π оберта | |||
| градусах | 180π ≈ 57.296° | |||
| градах | 200π ≈ 63.662 гон | |||
|
| ||||
Один радіан — це площинний кут, утворений двома радіусами, так, що довжина дуги між ними дорівнює радіусу кола. Тобто, вимірювання кута в радіанах показує в скільки разів довжина дуги кола, що спирається на цей кут, відрізняється від його радіуса.
Радіан є безрозмірнісною одиницею вимірювання та має позначення рад (міжнародне — rad)[4], але, зазвичай, при написанні це позначення не пишеться. При вимірюванні кутів в градусах використовують позначення °, для того щоб відрізнити від величин, виражених в радіанах.
Пояснення
Повна довжина кола дорівнює 2πr, де r — радіус кола. Тому повне коло є кутом в 2π≈6.28319 радіан. Перетворення радіанів у градуси та навпаки здійснюється так:
- рад ,
- 1 рад (або ) = .
- рад,
- рад рад.
Властивості
Широке застосування радіанів в математичному аналізі обумовлено тим, що вирази з тригонометричними функціями, аргументи яких вимірюються в радіанах, набувають максимально простого вигляду (без числових коефіцієнтів). Наприклад, використовуючи радіани, отримаємо просту тотожність
що лежить в основі багатьох елегантних формул в математиці.
При малих кутах синус і тангенс кута, вираженого в радіанах, рівні самому куту, що зручно при наближених обчисленнях.
Косинус малого кута, вираженого в радіанах, наближено дорівнює:
Розмірність
Радіан є безрозмірнісною одиницею вимірювання. Тобто числове значення кута, що виміряний в радіанах, позбавлене розмірності. Це легко бачити із самого означення радіана, як відношення довжини кола до радіуса. Згідно з рекомендаціями Міжнародного бюро з мір та ваг радіан інтерпретується як одиниця з розмірністю 1 = м·м−1 (м/м, тобто метр на метр — чисельник і знаменник можливо скоротити, тобто він має розмірність 1).
Інакше, безрозмірність радіана можна бачити з виразу ряду Тейлора для тригонометричної функції sin(x):
Якби x мав розмірність, тоді ця сума була б позбавлена змісту — лінійний доданок x не можна було б додати до кубічного x3/3!, як величини різних розмірностей. Отже, x мусить бути безрозмірнісним.
Див. також
Примітки
- 6.5.3 // Quantities and units—Part 1: General — 1 — ISO, 2009. — P. 18. — 41 p.
- Phillips W. D. Dimensionless units in the SI // Metrologia — IOP Publishing, 2014. — Vol. 52. — P. 40–47. — ISSN 0026-1394; 1681-7575 — doi:10.1088/0026-1394/52/1/40 — arXiv:1409.2794
- The International System of Units, Le Système international d’unités — 9 — BIPM, 2019. — ISBN 978-92-822-2272-0
- Наказ Міністерства економічного розвитку та торгівлі України від 25.08.2015 № 914. Про затвердження визначень основних одиниць SI, назв та визначень похідних одиниць SI, десяткових кратних і частинних від одиниць SI, дозволених позасистемних одиниць, а також їх позначень та Правил застосування одиниць вимірювання і написання назв та позначень одиниць вимірювання і символів величин.
Джерела
- Алєксєєв, В. М. Математика: Довідковий повторювальний курс [Текст] : [навч. посібник] / В. М. Алєксєєв, Р. П. Ушаков;за ред. М. Й. Ядренка. — К. : Вища школа, 1992. — 494 с. — ISBN 5-11-000094-1
- Математика для вступників до вузів [Текст] : навчальний посібник / В. В. Семенець, М. Ф. Бондаренко, В. А. Дікарев та ін. — Харків : СМІТ, 2002. — 1120с. — ISBN 966-7714-88-8. — ISBN 966-95983-1-1
Посилання
- Радіан // Термінологічний словник-довідник з будівництва та архітектури / Р. А. Шмиг, В. М. Боярчук, І. М. Добрянський, В. М. Барабаш ; за заг. ред. Р. А. Шмига. — Львів, 2010. — С. 165. — ISBN 978-966-7407-83-4.
- «Углы, градусы и радианы» — переклад статті Intuitive Guide to Angles, Degrees and Radians | BetterExplained (англ.)