Напівкубічна парабола

Напівкубічна парабола, або парабола Нейла — плоска алгебраїчна крива, що описується рівнянням

y^{2}=ax^{3}

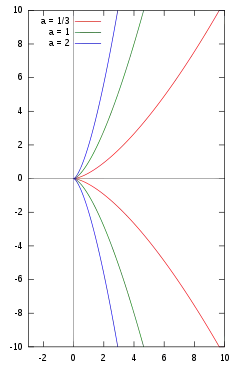
Напівкубічна парабола для різних значнь a.

в прямокутній системі координат. Параметричне рівняння напівкубічної параболи:

x=t^{2},\ y=at^{3}

Властивості

Окремим випадком напівкубічної параболи є еволюта параболи:

$x={3 \over 4}(2y)^{2 \over 3}+{1 \over 2}.$

Напівкубічна парабола є каустикою кривої Чирнгаузена. Більше того, будь-яка каустика вигляду ластівчин хвіт поблизу вершини добре наближається навікубічною параболою, що робить цю криву еталонною в теорії катастроф.
Радіус кривини навікубічної параболи в початку координат дорівнює нулю.

Історія

Названа по імені Нейла, який знайшов в 1657 р. довжину її дуги. Це була перша крива, довжину дуги якої вдалось порахувати. Також вдалось помітити особливість — тіло, що рухається вниз по напівкубічній кривій під дією сили тяжіння проходить однакові відстані у вертикальному напрямі за однакові проміжки часу.

Джерела

Weisstein, Eric W. "Semicubical Parabola." із сайту MathWorld--A Wolfram Web Resource.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.