Парабола

Пара́бола (від грец. παραβολή) — геометричне місце точок, що рівновіддалені від точки і прямої. Одна з кривих другого порядку.

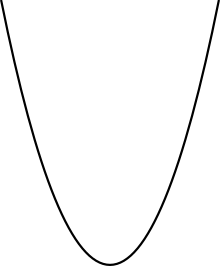
Точка зветься фокусом, а пряма — директрисою.

Парабола, гіпербола та еліпс є конічними перерізами. Парабола є конічним перерізом з одиничним ексцентриситетом. Якщо точкове джерело світла розміщене у фокусі параболоїдного дзеркала, то відбиті від поверхні промені будуть розповсюджуватися паралельно.

Графік функції, що задається за допомогою полінома другого степеня від однієї змінної, є параболою.

Історія

Параболічний циркуль, винайдений Леонардо да Вінчі

Найранішою відомою роботою із конічних перетинів є роботаМенехма в четвертому столітті до н. е.. Він знайшов спосіб вирішити задачу подвоєння куба із використанням парабол. (Але це рішення, однак, не відповідало вимогам щодо побудови за допомогою циркуля і лінійки.) Площа, що обмежена параболою і лінійним відрізком, так званий «параболічний сегмент», була розрахована Архімедом за допомогою метода вичерпування в третьому столітті до н. е., і виклав це в своїй роботі «Квадратура параболи». Назва «парабола» виникла завдяки Аполлонію, який дослідив багато властивостей конічних перетинів. Він означає «прикладання», що посилається на концепцію «прикладання або зіставлення площ», що має відношення і до цієї кривої, як довів Аполлоній.[1] Властивість фокуса і директриси параболи і інших конічних перетинів знайшов Папп Александрійський.

Галілео показав, що снаряд падає по параболічній траєкторії, що є наслідком постійного прискорення через дію сили тяжіння.

Ідея, що за допомогою параболічного рефлектора можна утворити зображення була відома задовго до винайдення першого рефлекторного телескопа.[2] Дизайн був запропонований на початку і в середині сімнадцятого століття багатьма математиками, серед яких були Рене Декарт, Марен Мерсенн,[3] і Джеймс Грегорі.[4] Коли Ісаак Ньютон в 1668 побудував перший рефлекторний телескоп, він не став використовувати параболічне дзеркало через складність його виготовлення, і обрав оптимальним сферичне дзеркало. Параболічні дзеркала використовуються у більшості сучасних рефлекторних телескопах, а також у супутникових тарілках і радіолокаторах.[5]

Визначення параболи як геометричного місця точок

Параболу можна визначити геометрично як множину точок (геометричне місце точок) в Евклідовому просторі:

Парабола це множина точок, таких, що для будь-якої точкиt $P$ в множині відстань $|PF|$ до фіксованої точки $F$ , фокусу, дорівнює відстані $|Pl|$ до фіксованої прямої $l$ , директриси:

\{P:|PF|=|Pl|\}

Середня точка $V$ утворена перпендикуляром із фокусу $F$ до директриси $l$ називається вершиною а пряма $FV$ віссю симетрії параболи.

Рівняння

Канонічне рівняння параболи в прямокутній системі координат:

\textstyle y^{2}=2px

(або

\textstyle x^{2}=2py

, якщо поміняти місцями осі).

Висновок

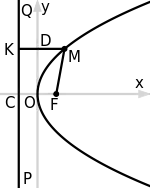Рівняння директриси $~PQ$ : $~\textstyle x+{\frac {p}{2}}=0$ , фокус — $~\textstyle F\left({\frac {p}{2}};0\right)$ , таким чином початок координат $~O$ — середина відрізу $~CF$ . За означенням параболи для будь-якої точки $~M$ , що лежить на ній виконується рівність $~KM=FM$ . $~\textstyle KM=KD+DM={\frac {p}{2}}+x$ і $~\textstyle FM={\sqrt {\left(x-{\frac {p}{2}}\right)^{2}+y^{2}}}$ , тоді рівність приймає вигляд:

~{\sqrt {\left(x-{\frac {p}{2}}\right)^{2}+y^{2}}}={\frac {p}{2}}+x

.

Після підняття в квадрат і деяких перетворень виходить рівносильне рівняння $~y^{2}=2px$ .

Квадратне рівняння $~y=ax^{2}+bx+c$ при $~a\neq 0$ також являє собою параболу і графічно зображаєтся тією ж параболою, що і $~y=ax^{2}$ , але на відміну від останньої має вершину не в початку координат, а в деякій точці $~A$ , координати якої обчислюються за формулами :

~x_{B}=-{\frac {b}{2a}},\;y_{B}=:-{\frac {D}{4a}}?\;y_{B}=F(x_{B})

Рівняння $~y=ax^{2}+bx+c$ може бути представлено у вигляді $~y=a(x-x_{A})^{2}+y_{A}$ , а у випадку переносу початку координат в точку $~A$ канонічним рівнянням. Таким чином для кожного квадратного рівняння можна знайти систему координат таку, що в цій системі воно представиться канонічним.

Розрахунок коефіцієнтів квадратного рівняння

Якщо для рівняння $~y=ax^{2}+bx+c$ відомі координати 3-х різних точок його графіка $~(x_{1};y_{1})$ , $~(x_{2};y_{2})$ , $~(x_{3};y_{3})$ , то його коефіцієнти можуть бути знайдені так:

$~a={\frac {y_{3}-{\frac {x_{3}(y_{2}-y_{1})+x_{2}y_{1}-x_{1}y_{2}}{x_{2}-x_{1}}}}{x_{3}(x_{3}-x_{1}-x_{2})+x_{1}x_{2}}},b={\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}-a(x_{1}+x_{2}),c={\frac {x_{2}y_{1}-x_{1}y_{2}}{x_{2}-x_{1}}}+ax_{1}x_{2}$

Властивості

Парабола — крива другого порядку.
Вона має вісь симетрії, що називається віссю параболи. Вісь проходить через фокус і перпендикулярна директрисі.
Оптична властивість. Пучок променів, паралельних осі параболи, відбиваючись у параболі, збирається в її фокусі. І навпаки, світло від джерела, що розміщене у фокусі, відображається параболою в пучок паралельних її осі променів.
Для параболи $y^{2}=x$ фокус розміщений у точці (0,25; 0).
Якщо фокус параболи дзеркально відобразити щодо дотичної, то його образ буде лежати на директрисі.
Парабола є антиподерою прямій.
Всі параболи подібні. Відстань між фокусом і директрисою визначає масштаб.
При обертанні параболи навколо осі симетрії виходить еліптичний параболоїд.
Еволютою параболи є напівкубічна парабола.

Побудова

Параболу y=ax²+bx+с будують за алгоритмом (через п'ять основних точок):

Визначити напрям рогів параболи за знаком першого коефіцієнта: a>0 — роги направлені вверх. Якщо a<0, то роги параболи направлені вниз.

Обчислити координати вершини параболи x₀= -b/2a і y₀=y(x₀)

Відмітити вершину параболи на координатній площині і через неї провести ось симетрії параболи x=x₀

Знайти точку перетину параболи з віссю OY (0;с) і відмітити їй симетричну

Розв'язати квадратне рівняння ax²+bx+с=0 і відмітити точки на осі OX (x₁;0) (x₂;0)

Через відмічені п'ять точок провести параболу.

Параболу можна побудувати «по точках», не знаючи рівняння і маючи в наявності тільки фокус і директрису. Вершина є серединою відрізка між фокусом і директрисою. На директрисі задається довільна система відліку з потрібним одиничним відрізком. Кожна наступна точка є перетином серединного перпендикуляра відрізка між фокусом і точкою директриси, що знаходиться на кратному одиничному відрізку відстані від початку відліку, і прямої, що проходить через цю точку і паралельна осі параболи.

Властивості дотичних

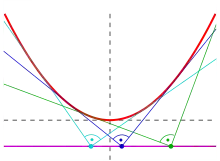
Перпендикулярні дотичні перетинаються на директрисі

Дві властивості пов'язані з фокальним параметром

Нехай лінія симетрії перетинає параболу в точці Q, точку фокуса позначимо як F а відстань від неї до точки Q позначимо як $f$ . Нехай перпендикуляр до лінії симетрії, що проходить крізь фокус, перетинає параболу в точці T. Тоді (1) відстань від F до T дорівнює $2 f$ , а (2) дотична до параболи в точці T перетинає лінію симетрії під кутом 45°.[6]^:p.26

Ортоптична властивість

Якщо дві дотичні параболи перпендикулярні одна одній, тоді вони перетинаються в точці на директрисі. І навпаки, дві дотичні, що перетинаються на директрисі — перпендикулярні.

Теорема Ламберта

Нехай три дотичні до параболи утворюють трикутник. Тоді теорема Ламберта стверджує, що фокус параболи знаходиться на колі, що описує трикутник.[7]^{:Corollary 20}

Парабола у декартовій системі координат

Вісь симетрії параболи паралельна осі y

Парабола: Визначення, p: половини фокусного параметру

Парабола: вісь паралельна осі y

Парабола: загальний випадок

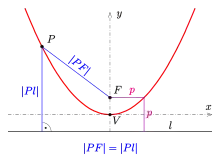
Якщо обрати декартові координати таким чином, що $F=(0,f)\ ,f>0,$ і деректриса матиме рівняння $y=-f$ отримаємо точку $P=(x,y)$ із $|PF|^{2}=|Pl|^{2}$ що задає рівняння $x^{2}+(y-f)^{2}=(y+f)^{2}$ . Розв'язавши його для $y$ отримаємо

y={\frac {1}{4f}}x^{2}

.

Парабола має U-подібну форму (відкриту до гори).

Довжина горизонтальної хорди, що проходить через точку фокусу (див. малюнок) називається фокусним параметром, половина якого є половиною фокусного параметру що позначається як $p$ . Із зображення отримаємо

p=2f

.

Фокусний параметр визначається аналогічним чином для еліпса і гіперболи. Для параболи $p$ це відстань від фокусу до директриси. Використовуючи параметр $p$ , рівняння параболи можна записати наступним чином

x^{2}=2py

.

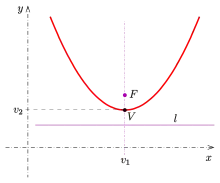
У більш загальному випадку, якщо вершина дорівнює $V=(v_{1},v_{2})$ , фокус $F=(v_{1},v_{2}+f)$ і директриса має рівняння $y=v_{2}-f$ отримаємо рівняння

y={\frac {1}{4f}}(x-v_{1})^{2}+v_{2}={\frac {1}{4f}}x^{2}-{\frac {v_{1}}{2f}}x+{\frac {v_{1}^{2}}{4f}}+v_{2}

.

Зауваження:

У випадку коли $f<0$ парабола відкрита вниз.
Припущення, що вісь симетрії паралельна осі y дозволяє розглядати параболу у вигляді графіку полінома із степенем 2 і навпаки: Графіком довільного полінома із степенем 2 є парабола.
Якщо замінити місцями $x$ і $y$ , отримаємо рівняння $y^{2}=2px$ парабол, в яких відкрита частина направлена ліворуч (якщо $p<0$ ) або праворуч (якщо $p>0$ ).

Загальний випадок

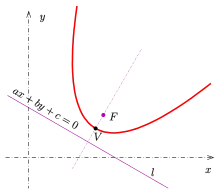
Якщо фокус дорівнює $F=(f_{1},f_{2})$ а директриса $ax+by+c=0$ отримаємо наступне рівняння

{\frac {\left(ax+by+c\right)^{2}}{a^{2}+b^{2}}}=\left(x-f_{1}\right)^{2}+\left(y-f_{2}\right)^{2}

(В лівій частині рівняння для розрахунку відстані $|Pl|$ використана Нормальна форма Гессе для прямої.)

неявне рівняння параболи визначено незвідним багаточленом із степенем два

ax^{2}+bxy+cy^{2}+dx+ey+f=0,

Парабола як графік функції

Графіки парабол

y=ax^{2}

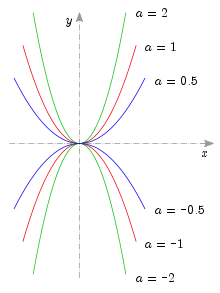
Будь-яку параболу із вершиною у початку координат і віссю $y$ , що є віссю симетрії параболи можна розглянути у вигляді графіку функції

f(x)=ax^{2}{\text{ with }}a\neq 0

.

Для $a>0$ направлено відкритою частиною в гору, а при $a<0$ відкрита вниз. Із попередніх розділів отримуємо:

Фокус це $\left(0,{\frac {1}{4a}}\right)$ ,
фокусна відстань — ${\frac {1}{4a}}$ , фокальний параметр дорівнює $p={\frac {1}{2a}}$ ,
вершина це $\left(0,0\right)$ ,
директриса має рівняння $y=-{\frac {1}{4a}}$ ,
дотична в точці $\left(x_{0},ax_{0}^{2}\right)$ має рівняння $y=2ax_{0}x-ax_{0}^{2}$ ,

Для $a=1$ парабола є одиничною параболою і задається рівнянням $y=x^{2}$ . Її фокусом є $\left(0,{\tfrac {1}{4}}\right)$ , фокальним параметр дорівнює $p={\tfrac {1}{2}}$ і директриса має рівняння $y=-{\tfrac {1}{4}}$ .

Загальний вигляд рівняння функції із степенем 2 буде наступним

f(x)=ax^{2}+bx+c{\text{ with }}a,b,c\in \mathbb {R} ,a\neq 0

.

Доповнюючи до повного квадрата, отримаємо

f(x)=a\left(x+{\frac {b}{2a}}\right)^{2}+{\frac {4ac-b^{2}}{4a}}

,

що є рівнянням параболі із

віссю $x=-{\frac {b}{2a}}$ (паралельною осі y),
фокусною відстанню ${\frac {1}{4a}}$ , і фокальним параметром $p={\frac {1}{2a}}$ ,
вершиною $V=\left(-{\frac {b}{2a}},{\frac {4ac-b^{2}}{4a}}\right)$ ,
фокусом $F=\left(-{\frac {b}{2a}},{\frac {4ac-b^{2}+1}{4a}}\right)$ ,
директрисою $y={\frac {4ac-b^{2}-1}{4a}}$ ,
точкою, в якій парабола перетинає вісь y матиме координати $\left(0,c\right)$ ,
дотична в точці на осі y матиме рівняння $y=bx+c$ .

Парабола як особливий випадок конічного перетину

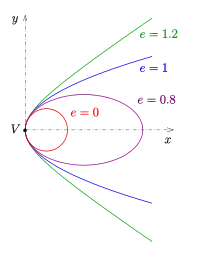
Конічні перетини із спільною вершиною

Родину конічних перетинів в яких вісь x є віссю симетрії, одна вершина знаходиться в початку координат (0,0) і які мають однакове значення половини фокусного параметру $p$ можна задати наступним рівнянням

y^{2}=2px+(e^{2}-1)x^{2}\qquad ,\ e\geq 0

,

де $e$ задає Ексцентриситет.

При $e=0$ конічним перетином є коло,
При $0<e<1$ — еліпс,
При $e=1$ — парабола із рівнянням $y^{2}=2px$ і
При $e>1$ буде отримана гіпербола (див. малюнок).

Парабола в полярних координатах

Родина конічних кривих із спільним фокусом

Якщо $p > 0$ , парабола із рівнянням $y^{2}=2px$ (із відритою частиною направленою праворуч) матиме полярні координати наступного вигляду:

r=2p{\frac {\cos \varphi }{\sin ^{2}\varphi }}{\text{ with }}\varphi \in \left[-{\tfrac {\pi }{2}},{\tfrac {\pi }{2}}\right]\setminus \{0\}.

(

r^{2}=x^{2}+y^{2},\ x=r\cos \varphi

.)

Її вершина матиме координати $V=(0,0)$ а фокус буде заданий як $F=\left({\tfrac {p}{2}},0\right)$ .

Якщо в початок координат розмістити фокус, тобто, $F=(0,0)$ , отримаємо рівняння

r={\frac {p}{1-\cos \varphi }}{\text{ with }}\varphi \neq 2\pi k.

Зауваження 1: Шляхом інвертування цієї полярної форми можна показати: що парабола це обернена до кардіоїди.

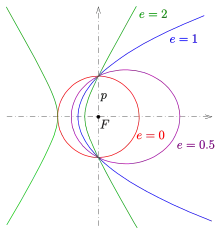
Зауваження 2: Друга форма полярних координат є особливим випадком із родини конічних перетинів із фокусом $F=(0,0)$ (див. зображення):

r={\frac {p}{1-e\cos \varphi }}

, (

e

: ексцентриситет).

Властивість відбивання променів

Рефлективна властивість параболи

Рефлективна властивість параболи означає що, якщо парабола може відбивати промені світла, тоді те світло, що потрапляє на неї і проходить паралельно осі симетрії відбивається в її точку фокуса. Цей висновок можна отримати із хвильової природи світла. Він правильний, але таке обґрунтування може бути недостатнім, аби бути математичним доказом. В наведеному далі доказі, факт, що кожна точка параболи є рівновіддаленою від фокусу і директриси приймається як аксіома.

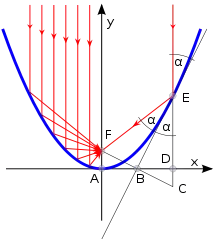
Розглянемо параболу $y = x 2$ . Оскільки всі параболи подібні, цей простий випадок відповідатиме усім іншим. Діаграма праворуч показує частину такої параболи.

Побудова і визначення

Точка E є довільною точку на параболі, із координатами $(x, x 2)$ . Фокус позначено як F, а вершину параболи як A (знаходиться у початку координат), а пряма FA (вісь $y$ ) є віссю симетрії. Пряма EC паралельна осі симетрії, і перетинає вісь $x$ в точці D. Точка C розміщена на директрисі (яка не показана, аби спростити діаграму). Точка B є серединою лінійного відрізку FC.

Дедукція

Якщо вимірювати здовж осі симетрії, вершина A є рівновіддаленою від фокусу F і від директриси. Відповідно до теореми Фалеса про пропорційні відрізки, оскільки C знаходиться на директрисі, $y$ -координати точки F і C є рівними за абсолютним значенням але мають протилежний знак. B є середньою точкою відрізку FC, тому її $y$ -координата дорівнює нулю, тому вона знаходиться на осі $x$ . Її $x$ -координата є половиною від значення координати точок E, D, і C, тобто, $x 2$ . Кутовий коефіцієнт прямого відрізку BE задається довжинами відрізків ED і BD, і становить $x 2 x /2$ , що зводиться до значення $2 x$ . Але $2 x$ є також кутових коефіцієнтом (першою похідною) параболи в точці E. Тому, пряма BE є дотичною до параболи в точці E.

Відстані EF і EC є рівними, оскільки E є точкою параболи, F є точкою фокусу а C — директриси. Тому, оскільки B є середньою точкою відрізку FC, трикутники △FEB і △CEB є конгруентними (по трьом сторонам), наслідком чого є те, що кути відмічені літерою $α$ є також конгруентними. (кут над E є вертикально протилежним кутом ∠BEC.) Це означає, що промінь світла, який потрапляє на параболу і проходить до точки E паралельно осі симетрії, буде відбиватися від прямої BE і в результаті буде слідувати по прямій EF, що показано червоним на малюнку (припускаючи що світло може відбиватися від прямих). Оскільки BE є дотичною до параболи в точці E, так само світло відбиватиметься від нескінченно малої ділянки дуги параболи в точці E. Таким чином, світло, яке потрапляє до параболи і проходить до точки E паралельно осі симетрії параболи відбивається параболою в точку фокусу.

Точка E не має особливих властивостей. Цей висновок щодо відбитого світла є вірним для усіх точок параболи, як показано в лівій частині зображення. Це є властивістю параболи.

Параболічні форми у природі, техніці та архітектурі

Траєкторії деяких космічних тіл (комет, астероїдів та інших), що проходять поблизу зорі або іншого масивного об'єкта на досить великій швидкості мають форму параболи (або гіперболи). Ці тіла внаслідок своєї великої швидкості і малої маси не захоплюються гравітаційним полем зорі і продовжують вільний політ. Це явище використовується для гравітаційних маневрів космічних кораблів (зокрема апаратів Вояджер).

При відсутності опору повітря траєкторія польоту тіла в однорідному гравітаційному полі є параболою.

При обертанні посудини з рідиною навколо вертикальної осі поверхня рідини в посудині і вертикальна площина перетинаються по параболі.

Властивість параболи фокусувати пучок променів, паралельних осі параболи, використовується в конструкціях прожекторів, ліхтарів, фар, а також телескопів-рефлекторів (оптичних, інфрачервоних, радіо тощо), в конструкції вузькоспрямованих (супутникових та інших) антен, необхідних для передавання даних на великі відстані, сонячних електростанцій і в інших галузях.

Форма параболи іноді використовується в архітектурі під час будівництва дахів і куполів.

Параболічна орбіта супутника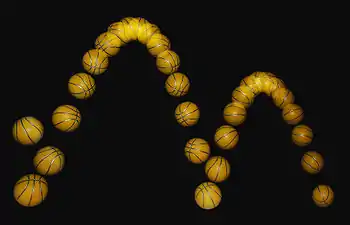
Падіння баскетбольного м'яча
Параболічна сонячна електростанція в Каліфорнії, США
Бібліотека з дахом у формі параболи, норвезьке місто Тромсьо
Параболічна форма поверхні рідини під час обертання. Дві рідини різної густини повністю заповнюють вузький простір між двома листами прозорого пластику. Проміжок між листами закрито знизу, з боків і зверху. Вся конструкція обертається навколо вертикальної осі, що проходить через центр.

Див. також

Джерела

Стаття в довіднику «Прикладная математика».
Анімовані рисунки, які ілюструють властивості параболи.
Інформация про связок параболи с фізикою.
Учебный фильм о параболе
Бронштейн И., Парабола, журнал"Квант, № 4, 1975.
А. А. Акопян, А. В. Заславский Геометрические свойства кривых второго порядка. Москва, Издательство МЦНМО, 2007 год.

Посилання

Парабола // Вища математика в прикладах і задачах / Клепко В.Ю., Голець В.Л.. — 2-ге видання. — К. : Центр учбової літератури, 2009. — С. 112-114. — 594 с.
Парабола // Термінологічний словник-довідник з будівництва та архітектури / Р. А. Шмиг, В. М. Боярчук, І. М. Добрянський, В. М. Барабаш ; за заг. ред. Р. А. Шмига. — Львів, 2010. — С. 145. — ISBN 978-966-7407-83-4.

Примітки

Can You Really Derive Conic Formulae from a Cone? - Deriving the Symptom of the Parabola - Mathematical Association of America. Процитовано 30 вересня 2016.
Wilson, Ray N. (2004). Reflecting Telescope Optics: Basic design theory and its historical development (вид. 2). Springer. с. 3. ISBN 3-540-40106-7. Extract of page 3
Stargazer, p. 115.
Stargazer, pp. 123 and 132
Fitzpatrick, Richard (14 липня 2007). Spherical Mirrors. Electromagnetism and Optics, lectures. University of Texas at Austin. Paraxial Optics. Процитовано 5 жовтня 2011.
Downs, J. W. (2003). Practical Conic Sections. Dover Publishing.^{[ISBN відсутній]}
Sondow, Jonathan (2013). The parbelos, a parabolic analog of the arbelos. American Mathematical Monthly 120: 929–935. arXiv:1210.2279. doi:10.4169/amer.math.monthly.120.10.929.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Can You Really Derive Conic Formulae from a Cone? - Deriving the Symptom of the Parabola - Mathematical Association of America. Процитовано 30 вересня 2016.

[2] Wilson, Ray N. (2004). Reflecting Telescope Optics: Basic design theory and its historical development (вид. 2). Springer. с. 3. ISBN 3-540-40106-7. Extract of page 3

[3] Stargazer, p. 115.

[4] Stargazer, pp. 123 and 132

[5] Fitzpatrick, Richard (14 липня 2007). Spherical Mirrors. Electromagnetism and Optics, lectures. University of Texas at Austin. Paraxial Optics. Процитовано 5 жовтня 2011.

[6] Downs, J. W. (2003). Practical Conic Sections. Dover Publishing.^{[ISBN відсутній]}

[7] Sondow, Jonathan (2013). The parbelos, a parabolic analog of the arbelos. American Mathematical Monthly 120: 929–935. arXiv:1210.2279. doi:10.4169/amer.math.monthly.120.10.929.