Основне рівняння руху потяга
Основне рівняння руху потяга (рівняння руху потяга) — фізичне рівняння, що встановлює зв'язок між активними і реактивними силами, що діють на елементи кінематичної системи — потяг, а також між кінематичними і силовими параметрами руху потяга. Фізичною основою для даного рівняння є другий закон Ньютона. Рівняння було вперше виведене М. Є. Жуковським.
Потяг як кінематична система
Потяг — це система, що складається із таких елементів: локомотива (-вів), вагонів (вагонеток), моторних і гальмівних секцій тощо. В кінематичному відношенні ці елементи зв'язані один з одним за допомогою зчіпних пристроїв, систем управління двигунами, гальмами тощо. Зазвичай, потяг переміщується по рейках, які утворюють т.з. колію, але в окремих випадках використовують і промислові автомобілі з причіпними секціями, — вони можуть розглядатися як потяг, що рухається по дорожньому покритті[1].
З позицій теорії, потяг — складна система, в яку входять багато елементів із пружними (пружно-дисипативними) і жорсткими зв'язками. Під пружними зв'язками розуміють зчіпні пристрої між елементами состава, під жорсткими — рейки (дорожнє покриття)[1].
Елементи потяга в період руху останнього виконують різні переміщення, які укрупнено поділяють на основні, тобто пов'язані із корисним переміщенням вантажу (уздовж колії), і додаткові (паразитні), які проявляються у вигляді обертання коліс, осей, елементів тягових пристроїв, коливальних процесів елементів состава, пов'язаних з нерівностями рейкової колії, системою підвіски локомотива і вагонів, подовжньою динамікою тощо. Кінематична єдність елементів потяга проявляється в однакових основних переміщеннях усіх елементів состава в кожний момент часу. Додатковими переміщеннями елементів состава при технологічному розрахунку залізничного (промислового локомотивного) транспорту зазвичай нехтують[1].
Сили, що діють на елементи потяга
Під час руху потяга, швидкість останнього змінюється від нуля до максимально можливого значення, і навпаки, тобто присутні прискорення, які є результатом дії різноманітних сил, які можуть бути як прикладені зовні (сила тяжіння, реакції від колії, опір від повітря тощо), так і ті, що виникають всередині складу (сили взаємодії між елементами потяга). Крім того, розрізняють сили, які керуються машиністом (сила тяги, сила гальмування і пов'язані з ними динамічні опори) і некеровані з боку машиніста (статичні сили опору руху).
Сили, що виникають при русі потяга, фігурують у рівняннях руху. За родом дії на рух елементів состава, сили можуть бути активними, реактивними та пасивними[1][2].
Активні сили виникають у стані спокою і руху потяга, діють в напрямі руху і прагнуть зрушити состав з місця або подовжити рух в певному напрямі. У рівняння руху підставляються зі знаком «+». Зазвичай, такі сили виражаються через результуючу силу тяги , яка виникає в результаті дії тягових пристроїв локомотива і моторних секцій (двигунів, рушіїв тощо).
Реактивні сили виникають лише при русі потяга і прагнуть перешкодити рухові. У загальному випадку, в рівняння руху реактивні сили підставляються зі знаком «–» (або зі знаком «+», але в різних із силою тяги частинах рівняння руху потяга). Мають різну природу і зазвичай зводяться до результуючої сили опору руху, яка залежить від величини состава (кількості вагонів або вагонеток), маси потяга, швидкості, стану і профілю рейкової колії, режиму руху потяга і дії гальмівних пристроїв тощо.
Опір руху може бути шкідливим (пов'язаний із тертям, зміною форми і розмірів складових елементів потяга тощо) і корисним (пов'язаний із подоланням перепаду висот між початковим і кінцевим пунктами прямування вантажу) . Шкідливий опір руху завжди перешкоджає руху потяга, і в рівнянні руху сили шкідливого опору завжди негативні. Під час руху состава на похилій ділянці колії виникає корисний опір руху — сила подовжньої складової сили власної ваги потяга, яка прагне перемістити состава вниз похилою площиною. Не дивлячись на свій активний характер, така складова традиційно причислюється до сил опору руху, і в рівняння руху потяга (тобто, в його частину із силою тяги) підставляється зі знаком «–» під час підйому, і зі знаком «+» — під час спуску состава.
.
Крім того, розрізняють статичний (постійний, притаманний рухові із постійною швидкістю) і динамічний (виникає додатково до статичного при зміні швидкості, за природою — завжди шкідливий) опори руху потяга. Сили динамічного опору руху потяга підставляються у рівняння (тобто, в його частину із силою тяги) зі знаком «–» у випадку розгону (збільшення швидкості) состава, і зі знаком «+» у випадку гальмування (зменшення швидкості) состава.
Пасивні сили діють перпендикулярно напряму руху, прямо не впливають на параметри руху потяга, але від їх значень залежать величини активних і реактивних сил. Зазвичай, це поперечні складові ваги елементів потяга.
Найпростіша комплектація потяга — із одним локомотивом у голові состава, структурну модель руху якого горизонтальною ділянкою колії наведено на рисунку.
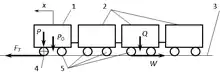
Отже, в загальному вигляді основне рівняння руху потяга можна записати наступним чином:
.
Форми запису основного рівняння руху потяга
Існують два записи основного рівняння руху потяга, які використовуються в розрахунках і наукових дослідженнях: в диференційній та в інтегральній формах[2][3].
Диференційна форма
,
де — сумарна сила тяги, що діє на приводні (моторні, рушійні) елементи потяга, Н;
— рівнодіюча статичних опорів руху, Н;
— приведена маса потяга, — ураховує масу частин, що рухаються поступно, а також інерцію частин, що обертаються[4], кг;
— маса потяга, кг;
— переміщення потяга, м;
— прискорення потяга (друга похідна переміщення по часі), м/с2;
— динамічний опір руху потяга, Н.
Аналіз основного рівняння руху потяга в диференційній формі[1]
Основне рівняння руху потяга містить 3 елементи: силу тяги (рівнодіюча активних сил), статичні опори руху (рівнодіюча реактивних сил, а також подовжньої складової власної ваги потяга, яка має активний характер) і динамічні опори руху (в залежності від режиму руху потяга можуть мати як активний, так і реактивний характер). Теоретично, кожен член рівняння може обертатися в нуль.
При — маємо випадок усталеного режиму руху потяга. Оскільки опори руху потяга і сила тяги в даному запису рівняння руху знаходяться у різних частинах рівняння, то при маємо випадок прискореного руху (розгону), при — уповільненого руху (вибігу — руху із вимкненими двигунами, або гальмування) потяга.
При — маємо окремий випадок, коли усі шкідливі опори руху компенсуються корисними, і локомотив розвиває тягу лише для розгону состава.
При — маємо випадок вільного вибігу состава, коли тягові пристрої вимкнені, а кінетична енергія потяга знижується при подоланні опорів руху.
Окремий випадок вибігу — гальмування состава, коли штучно, за допомогою спеціальних пристроїв, збільшують для зниження швидкості потяга до заданого значення або повної його зупинки.
За допомогою основного рівняння руху потяга в диференційній формі можна досліджувати основні рухи потяга. Крім того, рівняння надає можливість математичного опису поздовжньої динаміки потяга і додаткових рухів його елементів уздовж осі траси руху. В даному випадку основне рівняння руху в диференційній формі складають для кожного елементу потяга (із підстановкою у певне рівняння лише тих сил, що діють на певний елемент потяга), додаючи до названих вище сил зусилля у зчіпках состава. Для досягнення поставленої задачі розв'язують систему отриманих диференційних рівнянь другого порядку, кількість яких визначається кількістю елементів потяга[5].
Інтегральна форма
,
де — гальмівна сила, Н;
— вага локомотива (мотор-вагонного рухомого состава), Н;
— вага причіпної частини состава, Н;
— питомий опір руху потяга, Н/кН;
— питомий опір від ухилу колії, Н/кН, чисельно дорівнює ухилу колії, вираженому в проміле (‰). Оскільки даний опір знаходиться у різних частинах рівняння із силою тяги, то при русі потяга на ухил (тобто, на підйом), значення підставляється у рівняння зі знаком «+»; при русі з ухилу — зі знаком «–»;
— питомий опір руху потяга на криволінійних ділянках, діє лише на криволінійних ділянках маршруту прямування потяга, Н/кН. При оперуванні середньозваженим показниками, питомий опір та інші місцеві опори руху доцільно перерахувати у «фіктивний ухил» , який буде завжди позитивним і має діяти «на підйом состава» на всій протяжності маршруту потяга;
— питомий динамічний опір руху потяга, Н/кН. Оскільки даний опір знаходиться у різних частинах рівняння із силою тяги, то при розгоні состава питомий динамічний опір позитивний, при гальмуванні — негативний.
Добуток являє собою статичні опори руху в тягових режимах та вільному вибігу потяга, вираз — статичні опори в гальмівних режимах руху потяга. Добуток називають динамічним опором руху потяга.
Тобто, запис основного рівняння руху потяга в інтегральній формі містить у собі питомі параметри статичних і динамічних опорів руху потяга. Аналіз основного рівняння руху потяга в інтегральній формі дає ті ж самі результати, що й аналіз такого в диференційній формі. Дослідження основних рухів потяга за допомогою основного рівняння в диференційній та інтегральній формах дає аналогічні результати.
Примітки
- Волотковский С.А. (1981). Рудничная электровозная тяга. М.
- Тяга поездов.
- Поляков Н.С., Штокман И.Г. (1962). Основы теории и расчеты рудничных транспортных установок. М.
- Уравнение движения поезда. Коэффициент инерции вращающихся частей. Диаграмма удельных ускоряющих и замедляющих сил. Архів оригіналу за 26 січня 2019.
- Штокман И.Г. и др. (1986). Проектирование и конструирование транспортных машин и комплексов. М.
Джерела
- Гетьман Г. К. Теорія електричної тяги. У двох томах. Том I. — Дніпропетровськ: Акцент ПП, 2014. — 580 с.
- Деев В. В., Ильин Г. А., Афонин Г. С. Тяга поездов. — М.: Транспорт, 1987. — 264 с.
- Волотковский С. А. Рудничная электровозная тяга. — М.: Недра, 1981. — 389 с.
- Андреев А. В., Шешко Е. Е. Транспортные машины и комплексы для открытой добычи полезных ископаемых. — М.: Недра, 1970. — 430 с.
- Поляков Н. С., Штокман И. Г. Основы теории и расчеты рудничных транспортных установок. — М.: Госгортехиздат, 1962. — 491 с.