Петля (топологія)
Петля в топологічному просторі X— це неперервне відображення f одиничного відрізка I = [0,1] в X, таке що f(0) = f(1). Іншими словами, це шлях, початкова точка якого збігається з кінцевою[1].
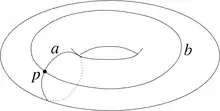
Петлю можна також розглядати як неперервне відображення f одиничного кола S1 в X, оскільки S1 можна вважати фактор-простором одиничного відрізка I при ототожненні 0 з 1.
Нехай X — топологічний простір, x0 ∈X. Неперервне відображення l: S1 → X, таке що l(1) = x0, називається круговою петлею в x0[2]. Кожній круговій петлі в точці x0 можна зіставити петлю простору X у тій самій точці, взявши композицію l з відображенням I →S1, заданим формулою t →e2πit. У такий спосіб з кругової петлі може бути отримана будь-яка петля.
Кругові петлі називаються гомотопними (або еквівалентними), якщо вони {1}-гомотопні (тобто, якщо гомотопія між ними є пов'язаною в точці 1 ∈ S1). Відповідні класи еквівалентності називаються гомотопічними класами петель.
Непорожній топологічний простір називається однозв'язним, якщо він лінійно зв'язний і будь-яка петля в ньому гомотопна постійній петлі[2].
Множина гомотопічних класів петель у точці утворює групу з операцією композиції шляхів. Ця група називається фундаментальною групою простору X у позначеній точці x0.
Множина всіх петель в X утворює простір, який називається простором петель простору X[1].
Див. також
- Вільна петля
- Група петель
- Простір петель
- Алгебра петель
- Фундаментальна група
- Квазігруппа
Примітки
- Adams, 1978, с. 3.
- Виро, Иванов, Нецветаев, Харламов, 2010, с. 232-234.
Література
- John Frank Adams. Infinite Loop Spaces. — Princeton University Press, 1978. — Т. 90. — (Annals of mathematics studies). — ISBN 9780691082066.
- О.Я. Виро, О.А. Иванов, Н.Ю. Нецветаев, В.М. Харламов. Элементарная топология. — М. : МЦНМО, 2010. — ISBN 978-5-94057-587-0.
