Неперервна функція
Непере́рвна фу́нкція — в математичному аналізі це функція у якої малим змінам аргумента відповідають малі зміни значення функції.
| Розділи в | ||||||
| Математичному аналізі | ||||||
|---|---|---|---|---|---|---|
|
||||||
|
||||||
|
||||||
|
||||||
|
Спеціалізовані |
||||||
Це означає, що графік неперервної функції не має стрибків, тобто може бути накреслений «не відриваючи олівець від паперу».
Всі елементарні функції — неперервні на своїй області визначення.
Неперервні функції трапляються набагато частіше, ніж диференційовні, множина всіх неперервних функцій замкнена відносно арифметичних операцій (за винятком ділення) і композиції та утворює чи не найважливіший клас функцій в аналізі.
Означення
проте є неперервною справа: : .
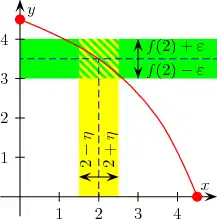
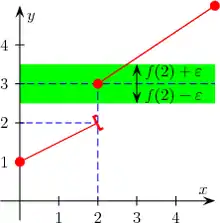
Функція дійсної змінної, яка означена в області , неперервна в точці якщо для довільного знайдеться таке (яке залежить від ), що з випливає
Функція неперервна в області , якщо неперервна в кожній точці цієї області.
Нехай — гранична точка множини A.
Означення неперервності в точці x0
Функція f називається неперервною в точці якщо:
- функція f(x) визначена в точці x0.
- існує границя
- .
Означення неперервності в точці x0 за Коші
Функція f називається неперервною в точці якщо:
Означення неперервності в точці x0 за Гейне
Функція f називається неперервною в точці якщо:
- .
Точки розриву
Якщо умова, що входить у визначення неперервності функції, в деякій точці порушується, то кажуть, що розглянута функція має в даній точці розрив. Інакше кажучи, якщо — значення функції в точці , то межа такої функції (якщо він існує) не збігається з . Мовою околів умова розривності функції в точці є запереченням умови неперервності розглянутої функції в даній точці, а саме: існує такий окіл точки в області значень функції , що як би ми близько не підходили до точки в області визначення функції завжди знайдуться такі точки, образи яких будуть за межами околу точки .
Класифікація точок розриву в R¹
Класифікація розривів функцій залежить від того, як влаштовані множини X та Y. Далі наведено класифікацію для найпростішого випадку функції . Подібним чином класифікують і особливі точки (точки, де функція не визначена).
Якщо функція має розрив в даній точці (тобто границя функції в даній точці відсутня або не збігається зі значенням функції в даній точці), то для числових функцій виникає два можливих варіанти, пов'язаних з існуванням у числових функцій односторонніх границь:
- якщо обидві односторонні границі існують і скінченні, то таку точку називають точкою розриву першого роду. До точок розриву першого роду відносять усувні розриви і стрибки.
- якщо хоча б одна з односторонніх границь не існує або не є скінченою величиною, то таку точку називають точкою розриву другого роду. До точок розриву другого роду відносять полюси і точки суттєвого розриву.
Усувна точка розриву
Якщо границя функції існує і скінченна, але функція не визначена в цій точці, або границя не збігається зі значенням функції в даній точці: , то точка називається точкою усувного розриву функції (в комплексному аналізі — усувна особлива точка). Якщо «виправити» функцію у точці усувного розриву і покласти , то вийде функція, неперервна в даній точці. Така операція над функцією називається довизначенням функції до неперервної або довизначенням функції за неперервністю, що і обґрунтовує назву точки, як точки усувного розриву.
Точка розриву «стрибок»
Розрив «стрибок» виникає, якщо
- .
Точка розриву «полюс»
Розрив «полюс» виникає, якщо однa з односторонніх границь нескінченнa.
- або .
Точка суттєвого розриву
У точці суттєвого розриву одна з односторонніх границь взагалі відсутня.
Класифікація ізольованих особливих точок в Rn, n>1
Для функцій та немає потреби працювати з точками розриву, але нерідко доводиться працювати з особливими точками (точками, де функція не визначена). Класифікація подібна.
- Якщо , то це усувна особлива точка (аналогічно функції дійсного аргументу).
- Полюс визначається як . В багатовимірних просторах, якщо модуль числа росте, вважається, що , яким шляхом б він не ріс.
- Якщо границя взагалі не існує, це суттєва особлива точка.
Поняття «стрибок» відсутнє. Те, що в вважається стрибком, в просторах більших розмірностей — суттєва особлива точка.
Властивості
Локальні
- Функція, неперервна в точці , є обмеженою в деякому околі цієї точки.
- Якщо функція неперервна в точці і (або ), то (або ) для всіх, досить близьких до .
- Якщо функції та неперервні в точці ,то функції та теж неперервні в точці .
- Якщо функції та неперервні в точці і при цьому , то функція теж неперервна в точці .
- Якщо функція неперервна в точці та функція неперервна в точці , то їх композиція неперервна в точці .
Глобальні
- Функція, неперервна на відрізку (або будь-якій іншій компактній множині ), рівномірно неперервна на ньому.
- Функція, неперервна на відрізку (або будь-якій іншій компактній множині), обмежена і досягає на ній своє максимальне і мінімальне значення.
- Областю значень функції , неперервної на відрізку , є відрізок де мінімум і максимум беруться по відрізку .
- Якщо функція неперервна на відрізку та то існує точка в якій .
- Якщо функція неперервна на відрізку і число задовольняє нерівності або нерівності то існує точка у котрій .
- Неперервне відображення відрізка в дійсну пряму ін'єктивне в тому і тільки в тому випадку, коли дана функція на відрізку строго монотонна .
- Монотонна функція на відрізку неперервна в тому і тільки в тому випадку, коли область її значень є відрізком з кінцями та .
- Якщо функції и неперервні на відрізку , причому та то існує точка в якій Звідси, зокрема, випливає, що будь-яке неперервне відображення відрізка в себе має хоча б одну нерухому точку.
Топологічні
Вивчення топологічних властивостей неперервних функцій відбувається шляхом їх розшарування на гомотопічні класи, де кожний клас складається з функцій, які можуть неперервно деформуватися одна в одну. Нехай та — топологічні простори, а та — неперервні функції, які відображають в . Відзначимо одиничний інтервал на дійсній прямій Тоді функції та є гомотопними, якщо існує неперервна функція , яка відображає у , для якої а Неперервна функція , яка описує неперервну деформацію функції у , називається гомотопією. Кожний гомотопічний клас характеризується степенем відображення яку називають топологічним індексом. Усі функції, які відображають у , можна розбити на гомотопічні класи, такі, що дві функції належать одному класові, якщо вони є гомотопними.
Приклади
Елементарні функції
Довільні многочлени , раціональні функції , показові функції , логарифми , тригонометричні функції (прямі і зворотні) неперервні скрізь у своїй області визначення.
Функція з усувним розривом
Функція задається формулою
неперервна в будь-якій точці Точка є точкою усувного розриву, бо границя функції
Функція знака
функція
називається функцією знака.
Ця функція неперервна в кожній точці .
Точка є точкою розриву першого роду , причому
- , в той час як в самій точці функція обертається в нуль.
Ступінчаста функція
Ступінчаста функція, яка визначається як
є всюди неперервна, крім точки , де функція терпить розрив першого роду. Проте, в точці існує правобічна границя, яка збігається зі значенням функції в даній точці. Таким чином, дана функція є прикладом неперервної справа функції на всій області визначення .
Аналогічно, ступінчаста функція, яка визначається як
є прикладом неперервної зліва функції на всій області визначення .
Функція Діріхле
функція
називається функцією Діріхле . По суті, функція Діріхле - це характеристична функція множини раціональних чисел . Ця функція є всюди розривної функцією , оскільки на кожному інтервалі існують як раціональні, так і ірраціональні числа.
Функція Рімана
функція
називається функцією Рімана або функцією Тома.
Ця функція є неперервною всюди у множині ірраціональних чисел (), оскільки границя функції в кожній точці дорівнює нулю.
Варіації і узагальнення
Рівномірна неперервність
Функція називається рівномірно неперервної на , якщо для будь-якого існує таке, що для будь-яких двох точок і яких, що , виконується .
Кожна рівномірно неперервна на множині функція, очевидно, є також і неперервною на ньому. Зворотне, взагалі кажучи, невірно. Однак, якщо область визначення - компакт, то неперервна функція виявляється також і рівномірно неперервною на даному відрізку.
Напівнеперервність
- Існує дві симетричні одна до одної властивості - напівнеперервна знизу і напівнеперервна зверху :
- функція напівнеперервна знизу в точці , якщо для будь-якого існує така околиця , що для будь-якого ;
- функція називається напівнеперервна зверху в точці , якщо для будь-якого існує такий окіл точки , що для будь-якого .
Між неперервністю і напівнеперервністю є такий зв'язок:
- якщо взяти функцію , неперервну в точці , і зменшити значення (на кінцеву величину), то ми отримаємо функцію, напівнеперервну знизу в точці ;
- якщо взяти функцію , неперервну в точці , і збільшити значення на кінцеву величину), то ми отримаємо функцію, напівнеперервну зверху в точці .
Відповідно до цього можна допустити для напівнеперервних функцій нескінченні значення:
- якщо , то будемо вважати таку функцію напівнеперервна знизу в точці ;
- якщо ,то будемо вважати таку функцію напівнеперервна зверху в точці .
Одностороння неперервність
Функція називається односторонньо неперервною зліва (справа) в кожній точці її області визначення, якщо для односторонньої границі виконується рівняння:
Неперервність майже всюди
На дійсній прямій зазвичай розглядається проста лінійна міра Лебега. Якщо функція така, що вона неперервна всюди на , крім, можливо, множини міри нуль, то така функція називається неперервною майже всюди .
У тому випадку, коли множина точок розриву функції не більше ніж зліченна, ми отримуємо клас інтегрованих за Ріманом функцій (див. Критерій інтегрованості функції за Ріманом).
Джерела
- Завало С. Т. (1972). Елементи аналізу. Алгебра многочленів. Київ: Радянська школа. с. 462. (укр.)
- Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — Москва : Наука, 1962. — Т. 1. — 607 с.(рос.)
- Функція неперервна // Універсальний словник-енциклопедія. — 4-те вид. — К. : Тека, 2006.
- Неперервність функції // Вища математика в прикладах і задачах / Клепко В.Ю., Голець В.Л.. — 2-ге видання. — К. : Центр учбової літератури, 2009. — С. 225. — 594 с.