Пластина (конструкція)

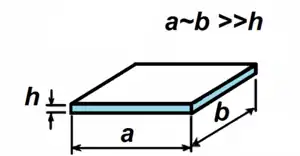
Пласти́на (англ. plate) — об'єкт, обмежений двома площинами, відстань між якими (товщина) є значно меншою від інших його розмірів[1]. У тому ж значенні, що і термін «пластина» також використовується термін «пластинка». З геометричної точки зору пластина може розглядатись як частковий випадок оболонки з радіусами кривини, які за величиною прямують до нескінченності.

Прямокутна пластина (h — товщина пластини)

Типи

Пластина — термін, що використовується у будівельній механіці для опису розрахункової схеми з врахуванням особливостей геометрії тіла. У випадку, коли один з розмірів тіла у декартовій системі координат значно відрізняється від двох інших, для спрощення розрахунку на міцність, жорсткість та стійкість реальна тривимірна конструкція може замінятись її розрахунковою схемою. Для пластин такою розрахунковою схемою є двовимірне плоске тіло, переміщення якого визначаються переміщеннями плоскої поверхні, яка є рівновіддаленою від поверхонь пластинки. Ця площина називається срединною площиною. При згинанні пластинки срединна площина перетворюється у вигнуту поверхню. Лінія перетину бокової поверхні пластинки із срединною площиною називається контуром пластинки. Наукова дисципліна, що розглядає теоретичні основи розрахунку пластин в умовах навантажень називається теорією пластин і оболонок.

Використані при означенні пластини поняття «значно менша» чи «значно відрізняється» не є достатньо визначеними. Залежно від особливостей навантаження пластини приймаються різні граничні співвідношення між товщиною та іншими розмірами пластини. Надійною умовою того, що будівельний об'єкт може розглядатись як пластина, є порівняння результатів розрахунку двома методами: як пластини і як плоского тривимірного тіла. Орієнтовно приймається умова, що для пластини її товщина є меншою за інші розміри не менше ніж у 5 разів. Тонка пластина, у якої максимальний прогин під дією поперечного навантаження перевищує чверть її товщини, називається гнучкою пластиною[2].

Пластина, що сприймає поперечне навантаження зазнаючи згину з власної площини, називається плитою. При розрахунку плити зазвичай використовуються два допущення: перше — приймається, що прямолінійні елементи, нормальні до срединної площини, залишаються після деформації прямими, нормальними до здеформованої срединної поверхні (гіпотеза прямих нормалей); друге — вважається, що пластинка є нестискуваною по товщині. Ці допущення дозволяють виразити переміщення усіх точок плити через поперечні переміщення срединної площини. Розрахунок пластин з використанням цих допущень становить основу технічної теорії згинання плит. Деформований стан плити, при якому серединна площина переходить у циліндричну поверхню, називається циліндричним згином, а така плита — балковою плитою.

Вертикально розташована пластинка, що перебуває в умовах плоского напруженого стану, називається стінкою або балкою-стінкою. Тонкі стінки за дії зовнішніх навантажень, прикладених паралельно до срединної поверхні, можуть втрачати місцеву стійкість. При перевірці стійкості тонких стінок, як і при розрахунку плит, використовується гіпотеза прямих нормалей.

Пластинки за конструкцією можуть бути одношаровими і багатошаровими (з двох і більше шарів). Пластинка, що має ребра, розташовані із сталим кроком в одному або двох напрямах, називається ребристою пластинкою. За наявності п'яти і більше ребер у кожному напрямі пластинка може розраховуватись як анізотропна конструкція. Ребриста прямокутна пластинка, ребра якої є паралельними до її сторін, називається ортотропною пластинкою.

Вивчення

Першим, хто започаткував розроблення теорії згинання й коливання пластин був Якоб Бернуллі молодший (1759–1789), який у 1789 році отримав диференціальне рівняння коливання пластини, розглядаючи її як систему струн, натягнутих у двох взаємно перпендикулярних напрямах[3]. Диференціальне рівняння зігнутої серединної поверхні пластини вперше було опубліковане Софі Жермен у 1816 році[4]. У 1828 році Оґюстен-Луї Коші (1789–1857), а згодом у 1829 Сімеон-Дені Пуассон (1781–1840) використали для розв'язування задачі про згинання пластин рівняння теорії пружності[5].

Густав Роберт Кірхгоф (1824—1887), німецький фізик, відомий своїми роботами з теорії розрахунку електричних кіл та деформації твердих тіл, у 1850 році розробив теорію згинання пластин. Запропонована ним теорія ґрунтується на двох припущеннях, що суттєво спрощують розрахунок: гіпотезі прямих нормалей і допущенні про нестискуваність матеріалу пластини по товщині. Ця теорія, що є розширенням принципів теорії балки Ейлера-Бернуллі на випадок пластин, згодом була розвинена англійським математиком А. Е. Г. Лавом (англ. Augustus Edward Hough Love; 1863—1940) на випадки коливань та деформацій пружних оболонок[6].

Корабельний інженер І. Г. Бубнов запропонував метод інтегрування диференціальних рівнянь при вирішенні крайових задач. Цей метод І. Г. Бубнов використав у 1902 році для розрахунку пластин, що працюють у системі корпуса корабля. Б. Г. Гальоркін, мабуть незалежно від І. Г. Бубнова, запропонував схожий метод інтегрування диференціальних рівнянь, який набув значного поширення для розрахунку прямокутних пластин при різних схемах навантаження і закріплення пластин. Метод отримав в технічній літературі назву «метод Бубнова-Гальоркіна».

Сучасні методи розрахунку пластин ґрунтуються на використанні методу скінченних елементів.

Застосування

Пластина може бути самостійною конструкцією або входити у склад пластинчастої системи. Окремі пластинки застосовують у будівництві у вигляді стінових панелей, балок-стінок, плит і панелей перекриттів і покриттів, фундаментних плит тощо.

Горизонтальні і вертикальні пластинки, що сполучені між собою в'язями, утворюють несучу систему, яку стосовно до будівель називають стіновою системою.

Похило розташовані пластинки можуть утворювати прогонові несучі конструкції. Система з прямокутних похилих пластинок, срединна поверхня яких розгортається на площину, називається складкою. Система з рівносторонніх трикутних або трепецієдальних пластинок, сполучених сторонами однакової довжини, називається шатровим покриттям або шатром.

Див. також

Примітки
  1. ДСТУ 2825-94 Розрахунки та випробування на міцність. Терміни та визначення основних понять.
  2. Уманский А. А. Справочник проектировщика промышленных, жилых и общественных зданий и сооружений. Расчётно-теоретический. Книга 2. М.: Стройиздат, 1973. — 416 с.
  3. Боголюбов А. Н. Бернулли Якоб II // Математики. Механики. Биографический справочник. К.: Наукова думка, 1983. — 640 c. — C.45.
  4. Mary Gray Sophie Germain (1776—1831) // Louise S. Grinstein; Paul Campbell. Women of Mathematics: A Bibliographic Sourcebook. Greenwood. — 1978. — P. 47–55. — ISBN 978-0-313-24849-8
  5. Григорьян А. Г. Механика от античности до наших дней. Издание 2-е переработанное и дополненное. — М.: Наука, 1974. — 482 с. — Серия «Из истории мировой культуры»
  6. A. E. H. Love On the small free vibrations and deformations of elastic shells // Philosophical trans. of the Royal Society (London), 1888, Vol. série A, N° 17 P. 491—549.

Посилання

Джерела
  • Феодосьев В. И. Сопротивление материалов: Учебник для вузов. — 10-е изд., перераб. и доп. — М. : Изд-во МГТУ им. Н. Э. Баумана, 1999. — Т. 2. — 592 с. — (Механика в техническом университете) — ISBN 5-7038-1340-9.
  • Timoshenko, S. and Woinowsky-Krieger, S. Theory of plates and shells. — McGraw–Hill New York, 1959.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.