Правило 72
Правило сімдесяти (правило 70)[1] — емпіричний спосіб наближеної оцінки терміну, в котрий певне значення зросте вдвічі при постійному зростанні на певний відсоток.
Згідно з «правилом сімдесяти»,
- ,
де r — річний відсоток зростання, T — термін (в роках) подвоєння суми. Наприклад, якщо на рахунок в банку вноситься певна сума грошей (наприклад, 1000 гривень) під r = 5 відсотків річних, то сума на рахунку подвоюється (до 2000 гривень) за термін приблизно рівний 14 рокам (T ≈ 70/5).
Множник 72 має більшу кількість дільників, що відповідають малим відсоткам (1, 2, 3, 4, 6, 8, 9, 12), і тому є більш зручним як ділене в порівнянні з більш точним значенням 69 та більш легким для запам'ятовування значенням 70. Тому правило має варіації як «Правило 70», так і як «Правило 72» (але може бути також і в варіації «Правило 69»).
Історія
Перша згадка про це правило з'являється в Луки Пачолі в його математичній праці «Сума арифметики, геометрії, дробів, пропорцій та пропорціональності», що вийшла в світ в 1494 році. Між тим, Пачолі не наводить розрахунків і не пояснює дане правило, що дозволяє зробити висновок, що правило це було відомо раніше.
Правило 70 як апроксимація
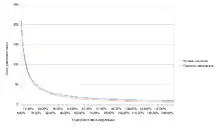
«Правило сімдесяти» є апроксимацією через гіперболу точної формули
Розклавши в ряд цей вираз для малих R, отримаєм . Переходячи від R частин цілого до відсотків (r = R*100), отримаєм . Так як ln 2 ≈ 0,693147, то найбільш точним серед цілих чисел при використанні малих відсотків є ділене 69.
Дві криві, що задаються цими функціями, досить добре збігаються (див. малюнок).
Похибка «правила сімдесяти»


Абсолютна похибка при використанні «правила сімдесяти» не перевищує чотирьох місяців, якщо річний відсоток r > 1,01 %.
При r = 2 % точна формула та «правило сімдесяти» дають майже ідентичні результати.
Відносна похибка починаючи з r = 2 % та вищє постійно зростає, досягаючи 9.86 % при r = 25 %.
Інші варіації правила
Замість 70 % також використовуються числа від 69 % до 72 %. Таким чином, згадуються «правило 69», «правило 70», «правило 71», «правило 72».
Інші варіанти використання
Правило сімдесяти може використовуватись не тільки для оцінки зросту грошових сум, але і для будь-яких інших процесів, що описуються експоненційним законом.
Тремін також не має обов'язково розраховуватись в роках; необхідною умовою є лише збіг одиниць вимірювання терміну відсотка зміни з одиницями вимірювання терміну подвоєння .
Крім того, значення не обов'язково має збільшуватись — воно може також зменшуватись на r відсотків за одиницю терміну. В цьому випадку оцінюється відповідно не термін подвоєння знаяння, а термін його зменшення вдвічі.
Зразки:
- Оцінка терміну, протягом якого ціни подвояється в результаті інфляції, якщо за рік вони ростуть на r відсотків.
- Тактова частота процесорів росте в средньому на r відсотків в місяць. За скільки місяців вона подвоїться? (див. закон Мура)
- За тисячу років кількість радіоактивного матеріалу в злитку зменшується на r відсотків. За який час кількість радіоактивного матеріалу скоротиться вдвічі? (див. Період напіврозпаду)