Правильний додекаедр
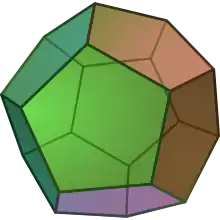
Правильний додека́едр (від грец. δώδεκα — дванадцять і грец. ἕδρα — грань) — правильний дванадцятигранник, об'ємна геометрична фігура, поверхня якої складена з дванадцяти правильних п'ятикутників. Кожна вершина додекаедра є вершиною трьох правильних п'ятикутників. Таким чином, додекаедр має 12 п'ятикутних граней, 30 ребер і 20 вершин (у кожній сходяться 3 ребра). Сума плоских кутів при кожній з 20 вершин рівна 324°.

Формули
Площа поверхні A і об'єм V додекаедра зі стороною a можна обчислити за формулами:
Радіус описаної сфери (сфери що проходить через всі вершини):
Радіус середньої сфери (сфери що проходить через центри всіх ребер):
ʀ
Радіус вписаної сфери (сфери що проходить через центри всіх граней):
Двогранний кут між гранями:
, де - золотий перетин
Приклади в природі
Деякі з правильних та напівправильних тіл зустрічаються у природі у вигляді кристалів, інші – у вигляді вірусів, чи найпростіших мікроорганізмів. Наприклад кристал піриту ( FeS ) – природна модель додекаедра.
Вірус поліомієліту має форму додекаедра.
Властивості
- Усі двадцять вершин додекаедра лежать по п'ять у чотирьох паралельних площинах, утворюючи в кожній з них правильний п'ятикутник.
- Двогранний кут між будь-якими двома суміжними гранями додекаедра дорівнює arccos (-1 / √5) ≈116 °, 565.
- Сума плоских кутів при кожній з 20 вершин дорівнює 324 °, тригранний кут дорівнює arccos (-11 / 5√5) ≈2,9617 стерадіан.
- У додекаедр можна вписати куб так, що сторони куба будуть діагоналями додекаедра.
- Додекаедр має три зірчасті форми.
Декартові координати
Якщо центр додекаедра збігається з початком координат, його вершини можна визначити за координатами: (±1, ±1, ±1): (0, ±1/φ, ±φ): (±1/φ, ±φ, 0): (±φ, 0, ±1/φ) де φ = (1+√5)/2 — золотий перетин. Довжина сторін тоді дорівнює 2/φ = −1+√5. Двогранний кут додекаедра становить 2arctan(φ) або приблизно 116,565 градусів.