Прямокутний тетраедр

Прямокутний тетраедр — це чотиригранник у якого всі ребра, прилеглі до однієї з вершин, перпендикулярні між собою.

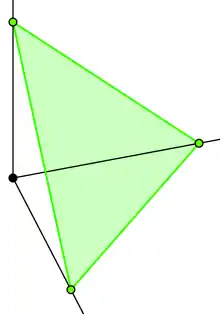
Прямокутний тетраедр може бути побудований з координат октанту і площини, що перетинає всі 3 осі від початку координат, як:

{\begin{cases}x>0&\\y>0&\\x>0&\\x/a+y/b+z/c<1&\end{cases}},

де a, b і c — коордитати точок перетину з осями x, y та z.

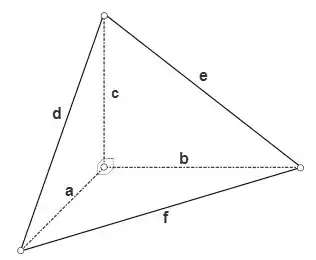
У прямокутному тетраедрі завжди три прилеглі грані будуть прямокутними трикутниками, а остання грань буде довільним трикутником і називається базою.

Формули

У прямокутного тетраедра з перпендикулярними гранями $a,b,c$ та вершиною в точці перетину перпендикулярних ребер (прямокутний тригранний кут):

$~V={\frac {1}{6}}abc$ (об'єм тетраедра);
$~S={\frac {1}{2}}{\sqrt {a^{2}b^{2}+b^{2}c^{2}+a^{2}c^{2}}}$ (площа основи тетраедра); Носить назву теореми де Гуа.
$~h={\frac {abc}{2S}};$ ${\frac {1}{h}}={\frac {1}{a^{2}}}+{\frac {1}{b^{2}}}+{\frac {1}{b^{2}}}$ (висота тетраедра, проведена з вершини прямокутного тригранного кута на основу, де S — це площа основи тетраедра);
$~R={\frac {1}{2}}{\sqrt {a^{2}+b^{2}+c^{2}}}$ (радіус сфери описаної навколо тетраедра);
$~r={\frac {ab+bc+ac+{\sqrt {a^{2}+b^{2}+c^{2}}}}{2(a+b+c)}}$ (радіус сфери, вписаної в тетраедр);
$~m={\frac {2}{3}}R;$ $~m={\frac {1}{3}}{\sqrt {a^{2}+b^{2}+c^{2}}}$ (медіана, проведена з вершини прямокутного тригранного кута, де R це — радіус сфери описаної навколо тетраедра);

Нехай площа основи $T_{0}$ і площи прямокутних граней відповідно $T_{1}$ , $T_{2}$ і $T_{3}$ , тоді

T_{0}^{2}=T_{1}^{2}+T_{2}^{2}+T_{3}^{2}.

Це є узагальненням теореми Піфагора на тетраедр.

Прямокутний тетраедр, натисніть тут для обертання моделі

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.