Правильний тетраедр
Тетра́едр називається правильним, якщо всі його грані — рівносторонні трикутники. У правильного тетраедра всі двогранні кути при ребрах і всі тригранні кути при вершинах рівні.
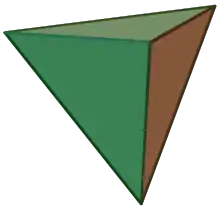
Тетраедр, натисніть тут для обертання моделі

Тривимірна модель правильного тетраедра
Декартові координати
Правильний тетраедр можна задати координатами його вершин
- (1, 1, 1)
- (-1, −1, 1)
- (-1, 1, −1)
- (1, −1, −1)
довжина ребра в цьому випадку складатиме .
Формули
У правильного тетраедра з довжиною ребра a:
Площа поверхні
Висота
Радіус вписаної сфери
Радіус описаної сфери
Кут нахилу ребра
Кут нахилу грані
Група симетрій — Тетраедральна (Th)
Властивості правильного тетраедра
- В правильний тетраедр можна вписати октаедр, притому чотири (з восьми) грані октаедра будуть суміщено з чотирма гранями тетраедра, всі шість вершин октаедра будуть суміщено з центрами шести ребер тетраедра.
- Правильний тетраедр з ребром х складається з одного вписаного октаедра (у центрі) з ребром х/2 і чотирьох тетраедрів (по вершинам) з ребром х/2.
- Правильний тетраедр можна вписати в куб двома способами, притому чотири вершини тетраедра будуть суміщено з чотирма вершинамі куба. Всі шість ребер тетраедра лежатимуть на всіх шести гранях куба і дорівнюватимуть діагоналі грані-квадрата.
- Правильний тетраедр можна вписати в ікосаедр, притому, чотири вершини тетраедра будуть суміщено з чотирма вершинамі ікосаедра.
У фізичному світі
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.