Розбіжні прямі

Прямі m. n. k. g - розбіжні

Розбіжними (гіперпаралельними, ультрапаралельними) прямими на гіперболічній площині називають прямі, які не перетинаються і не є паралельними.

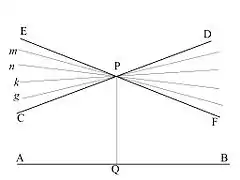
В гіперболічній геометрії згідно аксіоми паралельності на гіперболічній площині через точку Р, що не лежить на прямій АB, проходить більше однієї прямої, що не перетинають АB. Прямі, що не перетинають АB, заповнюють частину пучка з вершиною Р, яка лежить усередині пари вертикальних кутів EPC и DPF, розташованих симметрично відносно перпендикуляра PQ до прямої АB. Прямі, що утворюють сторони вертикальних кутів, відділяють прямі, що перетинають АB, від прямих, що її не перетинають і сами є такими, що не перетинають. Ці граничні прямі будуть паралельними в точці Р до прямої АB відповідно у двох її напрямках. Інші прямі, що не перетинають АB, називаються розбіжними з цією прямою.

• Атанасян Л.С. Геометрія Лобачевського = Геометрия Лобачевского. — Москва : Бином. Лаборатория знаний, 2014. — 464 с.
• Ефимов Н.В. Вища геометрія = Высшая геометрия. — Москва : Наука, 1978. — 576 с.
• Джесси Рассел. Геометрія Лобачевського = Геометрия Лобачевского. — Москва : Книга по Требованию, 2012. — 320 с.

• Прасолов В.В., Тихомиров В.М. Геометрія = Геометрия. — Москва : МЦНМО, 1997. — 352 с. (Книга в *.pdf та *.ps форматі.)

• А. С. Смогоржевский, «Про геометрію Лобачевського», Популярні лекції з математики, Випуск 23, Гостехиздат 1957 г., 68 ст. (рос.)
• Ф. Клейн, «Неевклідова геометрія.», М.-Л., ОНТИ, 1936, 356 с. (рос.)
• Н. Н. Іовлев, «Введение в элементарную геометрию и тригонометрию Лобачевского», М. -Л., Гиз, 1930 г., 67 с. (рос.)
• dic.academic.ru «ЛОБАЧЕВСКОГО ГЕОМЕТРИЯ» (рос.)