Геометрія Лобачевського

Прямі в моделі Кляйна. Через точку P проходить нескінченно багато прямих, які не перетинають пряму a.

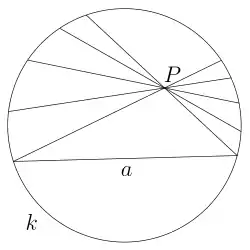
Точками моделі Кляйна є внутрішні точки круга одиничного радіусу з центром у початку координат. Відстань між точками ${\displaystyle a}$ і ${\displaystyle b}$ визначається за допомогою подвійного відношення, а саме як

${\displaystyle {\frac {1}{2}}\left|\ln {\left({\frac {x-a}{x-b}}:{\frac {y-a}{y-b}}\right)}\right|}$

для інтервалу ${\displaystyle (x,y)}$, де ${\displaystyle x}$ і ${\displaystyle y}$ — точки перетину прямої ${\displaystyle ab}$ з граничним колом круга.

Зазначимо, що точки граничного кола будуть нескінченно віддаленими точками площини Лобачевського. Граничне коло називають абсолютом або ідеальною межею.

У моделі Кляйна прямими є хорди кола[2]. Тому в цій моделі зручно розглядати питання пов'язані з опуклими множинами геометрії Лобачевського.

Перша фундаментальна форма площини Лобачевського в моделі Кляйна має вигляд[3]

${\displaystyle ds^{2}={\frac {(1-y^{2})\,dx^{2}+2xy\,dx\,dy+(1-x^{2})\,dy^{2}}{(1-x^{2}-y^{2})^{2}}}.}$

Аналогічним чином влаштована модель багатовимірного простору Лобачевського. Точками простору будуть внутрішні точки кулі одиничного радіусу, та точно так само, як і на площині, задається відстань подвійним відношенням.

Через точку площини проходять прямі, паралельні заданій прямій

Точками в моделі Пуанкаре в кулі ${\displaystyle \Delta ^{n}}$ будуть внутрішні точки кулі, а множиною нескінченно віддалених точок (абсолютом) буде гранична сфера. Прямими в цій моделі будуть дуги кіл та відрізки, ортогональні абсолюту. Метричними сферами в цієї моделі будуть евклідові сфери, які лежать в кулі ${\displaystyle \Delta ^{n}}$ (зауважимо, що взагалі центри сфер зміщені відносно центрів евклідових сфер).

Це конформна модель геометрії Лобачевського, тобто кут між кривими в цій моделі збігається з евклідовим кутом.

Перша фундаментальна форма простору Лобачевського в моделі Пуанкаре в кулі має вигляд[3]

${\displaystyle ds^{2}={\frac {4(dx_{1}^{2}+\dots +dx_{n}^{2})}{(1-x_{1}^{2}-\dots -x_{n}^{2})^{2}}}.}$

Точками в моделі Пуанкаре у верхній півплощині ${\displaystyle \mathbb {H} ^{n}}$ будуть внутрішні точки півпростору ${\displaystyle \mathbb {H} ^{n}=\{(x_{1},\dots ,x_{n})\in \mathbb {R} ^{n}|\ x_{n}>0\}}$, а множиною нескінченно віддалених точок (абсолютом) буде гіперплощина ${\displaystyle x=0\cup \infty }$. Прямими в цій моделі будуть дуги кіл і промені ортогональні абсолюту. Метричними сферами в цій моделі будуть звичайні евклідові сфери.

Перша фундаментальна форма простору Лобачевського в моделі Пуанкаре у верхній півплощині має вигляд[4]

${\displaystyle ds^{2}={\frac {dx_{1}^{2}+\dots +dx_{n}^{2}}{x_{n}^{2}}}.}$

Як і модель Пуанкаре в кулі, це також конформна модель геометрії Лобачевського. Існує конформне перетворення, яке перетворює одну модель в іншу.