Рухи Пахнера
Рухи Пахнера, названі ім'ям Удо Пахнера, — це методи заміни тріангуяції кусково-лінійного многовиду іншою тріангуляцією гомеоморфного многовиду. Рухи Пахнера називають також бізірковими перебудовами. Будь-які дві тріангуляції кусково-лінійного многовиду пов'язані скінченною послідовністю рухів Пахнера.
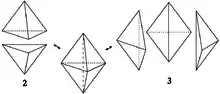
2-3 рух Пахнера: об'єднання 2 тетраедрів розбивається на 3 тетраедри.
Визначення
Нехай — -симплекс, а — комбінаторна n-сфера з тріангуляцією у вигляді межі n+1-симплекса.
Якщо задано тріангульований кусково-лінійний n-многовид і підкомплекс з корозмірністю 0 разом зі симпліціальним ізоморфізмом , рух Пахнера на N, асоційований із C, це тріангульований многовид . За побудовою цей многовид PL-ізоморфний , але ізоморфізм не зберігається тріангуляції.
Примітки
Література
- Udo Pachner. P.L. homeomorphic manifolds are equivalent by elementary shellings // European Journal of Combinatorics. — 1991. — Т. 12, вип. 2 (24 травня). — С. 129–145. — DOI:.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.