Симплекс

Як відомо, через будь-які n точок можна провести (n-1)-площину і існують множини з n+1 точок, через які (n-1)-площину провести не можна. Таким чином n+1 — мінімальна кількість точок в n-просторі, які не лежать в одній (n-1)-площині, і можуть бути вершинами n-многогранника, тобто, n-симплекс являє собою джойн n+1 точок.

Простий n-многогранник з кількістю вершин n+1 називається симплексом. У просторах найменших розмірностей цьому визначенню відповідають 4 фігури:

• 0-симплекс (точка) — 1 вершина;
• 1-симплекс (відрізок) — 2 вершини;
• 2-симплекс (трикутник) — 3 вершини;
• 3-симплекс (тетраедр) — 4 вершини.

Всі ці фігури володіють трьома загальними властивостями:

1. Відповідно до визначення, число вершин у кожної фігури на одиницю більше розмірності простору;
2. Існує загальне правило перетворення фігур нижчої розмірності у фігури вищої розмірності. Воно полягає в тому, що з геометричного центра фігури будується перпендикуляр в наступний вимір, на цьому перпендикулярі будується нова вершина і з'єднується ребрами зі всіма вершинами початкового симплексу;
3. Як випливає з описаної в п. 2 процедури, будь-яка вершина симплекса сполучена ребрами зі всією рештою вершин.

Симплекс має n+1 вершин, кожна з яких сполучена ребрами зі всією рештою вершин.

Оскільки всі вершини симплексу сполучені між собою, то тією ж властивістю володіє і будь-яка підмножина його вершин. Це значить, що будь-яка підмножина з L+1 вершин симплексу визначають його L-вимірну грань, і ця грань сама є L-симплексом. Тоді для симплексу число L-вимірних граней рівне числу способів вибрати L+1 вершину з повного набору n+1 вершин.

Позначимо символом K(L, n) число L-вимірних граней в n-многограннику, тоді для n-симплексу

${\displaystyle ~K(L,n)=C_{n+1}^{L+1},}$

де ${\displaystyle ~C_{n}^{m}}$ — число комбінацій з n по m.

Зокрема, кількість граней найбільшої розмірності рівна кількості вершин і рівна n+1:

${\displaystyle ~K(0,n)=K(n-1,n)=n+1.}$

Зелений трикутник — стандартний 2-симплекс

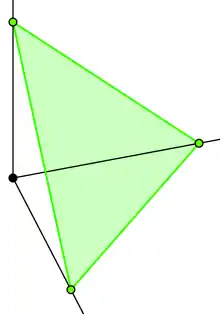
Стандартний n-симплекс ця підмножина ${\displaystyle \mathbb {R} ^{n+1}}$, що визначається як:

${\displaystyle \Delta ^{n}=\{(t_{0},\dots t_{n})\mid {(\sum _{i}t_{i}=1)}\wedge {(\forall i\;t_{i}\geqslant 0)}\}}$

Його вершинами є точки:

e₀=(1, 0 . 0): e₁=(0, 1 . 0)

.

e_n=(0, 0 . 1)

Існує канонічне бієктивне відображення стандартного n-симплекса в будь-якій іншої n-симплекс з координатами вершин ${\displaystyle (v_{0},v_{1},\dots v_{n})}$:

${\displaystyle (t_{0},\dots t_{n})\to \sum _{i}t_{i}v_{i}}$

Значення t_i для даної точки називаються її барицентричними координатами.

Альтернативну координатну систему можна визначити взявши:

${\displaystyle {\begin{aligned}s_{0}&=0\\s_{1}&=s_{0}+t_{0}=t_{0}\\s_{2}&=s_{1}+t_{1}=t_{0}+t_{1}\\s_{3}&=s_{2}+t_{2}=t_{0}+t_{1}+t_{2}\\&\dots \\s_{n}&=s_{n-1}+t_{n-1}=t_{0}+t_{1}+\dots +t_{n-1}\\s_{n+1}&=s_{n}+t_{n}=t_{0}+t_{1}+\dots +t_{n}=1\end{aligned}}}$

Тоді точки симплекса визначаються векторами з неспадними координатами між 0 and 1:

${\displaystyle \Delta _{*}^{n}=\left\{(s_{1},\cdots ,s_{n})\in \mathbb {R} ^{n}\mid 0=s_{0}\leq s_{1}\leq s_{2}\leq \dots \leq s_{n}\leq s_{n+1}=1\right\}.}$

Симплекс називається правильним, якщо всі його ребра мають однакову довжину: наприклад, правильний трикутник або правильний тетраедр. Правильний симплекс завжди є правильним многогранником.

Орієнтований об'єм n-симплекса в n-вимірному евклідовому просторі можна визначити за формулою:

${\displaystyle V={\frac {1}{n!}}\det(v_{1}-v_{0},v_{2}-v_{0},\dots ,v_{n}-v_{0})}$

Визначник Келі-Менгера дозволяє обчислити об'єм симплексу, знаючи довжини його ребер:

${\displaystyle V^{2}={\frac {(-1)^{n-1}}{2^{n}(n!)^{2}}}{\begin{vmatrix}0&1&1&1&\dots &1\\1&0&d_{01}^{2}&d_{02}^{2}&\dots &d_{0n}^{2}\\1&d_{10}^{2}&0&d_{12}^{2}&\dots &d_{1n}^{2}\\1&d_{20}^{2}&d_{21}^{2}&0&\dots &d_{2n}^{2}\\\vdots &\vdots &\vdots &\vdots &\ddots &\vdots \\1&d_{n0}^{2}&d_{n1}^{2}&d_{n2}^{2}&\dots &0\\\end{vmatrix}}}$

де ${\displaystyle d_{ij}=|v_{i}-v_{j}|}$ — відстань між i-й і j-й вершинами, n — розмірність простору. Ця формула — узагальнення формули Герона для трикутників.

Об'єм правильного n-симплекса з одиничною стороною рівний ${\displaystyle {\frac {\sqrt {n+1}}{n!\,2^{n/2}}}}$

Якщо задано ${\displaystyle ~C_{n+1}^{2}}$ додатних дійсних чисел ${\displaystyle d_{ij},~0\leq i,j\leq n,}$ то симплекс відстань між відповідними вершинами якого рівна цим числам існує тоді і тільки тоді, коли ${\displaystyle X^{T}DX<0,\quad \forall X:\sum _{i=0}^{n}x_{i}=0,}$ де матриця D визначається:

${\displaystyle D={\begin{pmatrix}0&d_{01}^{2}&d_{02}^{2}&\dots &d_{0n}^{2}\\d_{10}^{2}&0&d_{12}^{2}&\dots &d_{1n}^{2}\\d_{20}^{2}&d_{21}^{2}&0&\dots &d_{2n}^{2}\\\vdots &\vdots &\vdots &\vdots &\ddots &\vdots \\d_{n0}^{2}&d_{n1}^{2}&d_{n2}^{2}&\dots &0\\\end{pmatrix}}.}$

Еквівалентно такий симплекс існує, якщо і тільки якщо квадратна матриця A розмірності n елементи якої визначаються:

${\displaystyle a_{ij}={\begin{cases}d_{0i}^{2},&i=j\\{\frac {d_{0i}^{2}+d_{0j}^{2}+d_{ij}^{2}}{2}},&i\neq j\end{cases}}}$

є додатноозначеною. Дана матриця є матрицею Грама для векторів ${\displaystyle v_{1}-v_{0},v_{2}-v_{0},\dots ,v_{n}-v_{0}.}$

Число L-мірних граней	${\displaystyle ~K(L,n)=C_{n+1}^{L+1}}$
Висота	${\displaystyle ~H_{n}=a{\sqrt {\frac {n+1}{2n}}}}$	${\displaystyle ~H_{n}=R_{n}{\frac {n+1}{n}}}$	${\displaystyle ~H_{2}=a{\frac {\sqrt {3}}{2}}}$	${\displaystyle ~H_{3}=a{\frac {\sqrt {6}}{3}}}$	${\displaystyle ~H_{4}=a{\frac {\sqrt {10}}{4}}}$
Об'єм	${\displaystyle ~V_{n}={\frac {a^{n}}{n!}}{\sqrt {\frac {n+1}{2^{n}}}}}$	${\displaystyle ~V_{n}={\frac {R_{n}^{n}}{n!}}{\sqrt {\left({\frac {n+1}{n}}\right)^{n}}}}$	${\displaystyle ~V_{2}=a^{2}{\frac {\sqrt {3}}{4}}}$	${\displaystyle ~V_{3}=a^{3}{\frac {\sqrt {2}}{12}}}$	${\displaystyle ~V_{4}=a^{4}{\frac {\sqrt {5}}{96}}}$
Радіус описаної сфери	${\displaystyle ~R_{n}=a{\sqrt {\frac {n}{2(n+1)}}}}$	${\displaystyle ~a=R_{n}{\sqrt {\frac {2(n+1)}{n}}}}$	${\displaystyle ~R_{2}=a{\frac {\sqrt {3}}{3}}}$	${\displaystyle ~R_{3}=a{\frac {\sqrt {6}}{4}}}$	${\displaystyle ~R_{4}=a{\frac {\sqrt {10}}{5}}}$
Радіус вписаної сфери	${\displaystyle ~r_{n}={\frac {a}{\sqrt {2n(n+1)}}}}$	${\displaystyle ~r_{n}={\frac {R_{n}}{n}}}$	${\displaystyle ~r_{2}=a{\frac {\sqrt {3}}{6}}}$	${\displaystyle ~r_{3}=a{\frac {\sqrt {6}}{12}}}$	${\displaystyle ~r_{4}=a{\frac {\sqrt {10}}{20}}}$
Двогранний кут	${\displaystyle ~\cos \alpha ={\frac {1}{n}}}$

Співвідношення між величинами:

${\displaystyle ~R_{n}=H_{n}{\frac {n}{n-1}}}$

${\displaystyle ~a^{2}=H_{n}^{2}+R_{n-1}^{2}}$

${\displaystyle ~V_{n}={\frac {1}{n}}V_{n-1}H_{n}}$

${\displaystyle ~r_{n}=R_{n}^{2}-R_{n-1}^{2}}$

• Симплекс-метод
• Симпліціальний комплекс
• Симпліціальний багатогранник

• Александров П. С., Комбинаторная топология, М. — Л., 1947
• Понтрягин Л. С., Основы комбинаторной топологии, М. — Л., 1947, с. 23—31.

• Weisstein, Eric W. Симплекс(англ.) на сайті Wolfram MathWorld.