Рівномірне розфарбування
Рівномірне розфарбування в теорії графів — це приписування кольорів вершинам неорієнтованого графу, таким чином, що
- Ніякі дві суміжні вершини не мають однаковий колір,
- Число вершин у будь-яких двох колірних класах відрізняються більш ніж на одиницю.
Тобто, це процес розбиття вершин на різні кольори якомога більш рівномірним чином. Наприклад, для рівномірності слід давати кожній вершині свій власний колір, що призводить до того, що зазвичай, використовують набагато більше кольорів, ніж необхідно для оптимального розфарбування. Еквівалентний спосіб визначення рівномірного розфарбування є вкладенням даного графу як підграфу графу Турана. Є два види хроматичних чисел, які пов'язані з рівномірним розфарбуванням.[1] Рівномірним хроматичним числом графу G називається найменше число k, при якому G має рівномірне розфарбування з k кольорів. Але G може не мати рівномірного розфарбування для деякого великого числа кольорів; рівномірний хроматичний поріг G є найменше число k, при якому G має рівномірне розфарбування для будь-якої кількості кольорів більшої або рівної k.[2]
Теорема Хайнала-Семереді, подається як гіпотеза Ердеша (1964) і доведена Хайналом і Семереді (1970). Вона стверджує, що будь-який граф з максимальною степенню Δ має рівномірне розфарбування з Δ + 1 кольорів. Для знаходження розфарбування застосовуються алгоритми поліноміального часу, ці алгоритми використовуються також для знаходження оптимального розфарбування спеціальних класів графів,[3] але є більш загальна проблема — чи має довільний граф NP-повне рівномірне розфарбування із заданою кількістю кольорів.
Приклади
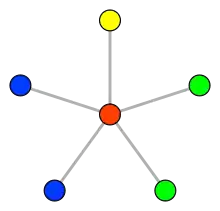
Граф-зірка K1,5, що показана на малюнку, є повним дводольним графом, і, отже, може бути пофарбована в два кольори. Проте, у результаті такого розфарбування цей граф має одну вершину в одному кольоровому класі та п'ять в іншому, і тому таке розфарбування є нерівномірним. Найменше число кольорів в рівномірному розфарбуванні цього графу дорівнює чотирьом, як показано на малюнку: центральна вершина повинна бути єдиною вершиною в її колірному класі, так що інші п'ять вершин повинні бути розділені щонайменше на три колірних класи, аби гарантувати, що інші колірні класи мають не більше двох вершин. Таким чином, хроматичне число графу може відрізнятися від його рівномірного забарвлення на n/4. Оскільки K1,5 має максимальну степінь п'ять, кількість кольорів гарантованих для нього по теоремі Хайнала-Семереді — шість, досягається шляхом надання кожній вершині свого кольору.
Теорема Хайнала-Семереді
Теорема Брукса свідчить, що будь-який зв'язний граф з максимальною степенню Δ має Δ-розфарбування, з двома винятками (повні графи і непарні цикли). Проте, це розфарбування може бути в цілому далеке від рівномірного. Ердеш (1964) зробив припущення, що рівномірне розфарбування можливе тільки з більш ніж одним кольором: будь-який граф з максимальною Δ-степенню має рівномірне розфарбування з Δ + 1 кольорів. Випадок Δ = 2 є простим (будь-яке об'єднання шляхів і циклів може бути справедливо розфарбованно з використанням повторного малюнка з трьох кольорів, з незначними змінами до повторення при закритті циклу) і випадок Δ + 1 = n/3 був вирішений раніше методом Корраді та Хайнала (1963). Повна гіпотеза була доведена Хайналом та Семереді (1970), і у даний час відома як теорема Хайнала-Семереді. Поліноміальний алгоритм часу для знаходження рімномірного розфарбування з великою кількістю кольорів був описаний у методі Кієрстада-Косточки. Кієрстад та Косточка також сформулювали, але не довели, посилення теореми, яка показує, що рівномірне k-розфарбування існує щоразу, коли кожні дві суміжні вершини мають такі степіні, що їх сума більше ніж 2k + 1.
Мейер висловив припущення з теореми Брукса для рівномірного забарвлення: кожен зв'язний граф з максимальною Δ-степеню має рівномірне розфарбування з Δ чи меншою кількістю кольорів, за винятком повних графів і непарних циклів. Посилений варіант гіпотези стверджує, що кожен такий граф має рівномірне розфарбування з точно Δ кольорів, з одним додатковим винятком, повний дводольний граф, в якому обидві дводольні сторони мають однакове непарне число вершин.[1]
Сеймур (1974) запропонував посилення теореми Хайнала-Семереді, до якого можна також віднести теорему Дірака, що щільні графи — Гамільтонові: він висловив припущення, що, якщо кожна вершина в n-вершинному графі має хоча б kn/(k + 1) сусідів, тоді граф містить в ролі підграфу граф, утворений шляхом з'єднання вершин, які знаходяться у k кроках одна від одної в n-циклі. Випадок k = 1 є теоремою Дірака. Теорема Хайнала-Семереді може бути взята з цієї гіпотези шляхом застосування гіпотези для великих значень k до доповнення графу, даного графу, і з використанням як кольорів класів суміжних підпослідовностей вершин з n-циклу. Гіпотеза Сеймура була доведена для графу, в якому n досить велике по відношенню до k; доказ використовує кілька складних фактів, включаючи саму теорему Хайнала-Семереді.
Спеціальні класи графів
Для будь-якого дерева з максимальною степеню Δ, рівномірне хроматичне число щонайбільше
Проте, більшість дерев мають значно менші рівномірні хроматичні числа: якщо дерево з n вершинами має Δ ≤ n/3 − O(1), то воно має рівномірне розфарбування тільки з трьома кольорами. Фурманчук (2006) вивчає рівномірне хроматичне число добутку графів.
Проблематика рівномірного розфарбовування
Також була розглянута проблема знаходження рівномірного розфарбування з найменшою кількістю кольорів. Перехід від розфарбування графу до рівномірного розфарбування можна довести додаванням достатньої кількості ізольованих вершин графу, таким чином, щоб граф був NP-повним, це потрібно для перевірки того, що граф має рівномірне розфарбування з заданою кількістю кольорів (більше двох). Проте, ця проблема стає все більш цікавою, коли обмежується спеціальними класами графів або параметризацією. Бодлендер та Фомін (2005) показали, що якщо нам дано граф G і число с кольорів, тоді можна перевірити, чи допускає G справедливе с-розфарбування в часі O(nO(t)), де t деревна ширина G; зокрема, рівномірне забарвлення може бути отримане оптимальним чином за поліноміальний час для дерев (раніше відомі по Чен та Лі 1994) і зовніпланарних графів. Алгоритм поліноміального часу також використовується для рівномірного забарвлення розщеплюваних графів.
Додатки
Одним з прикладом застосування рівномірного розфарбування запропонованого Мейером (1973) є рішення задачі про планування завдань. У цій задачі вершини графу являють собою набір завдань, які повинні бути виконані, і ребро з'єднує два завдання, які не повинні виконуватися одночасно. Розфарбування цього графу являє собою розбиття задач на підмножини, які можуть виконуватися одночасно; Таким чином, кількість кольорів у розфарбуванні відповідає кількості часових кроків, необхідних для виконання всього завдання. З міркувань балансування навантаження, бажано виконувати рівні або майже рівні кількості завдань на кожному кроці, і це балансування саме те, що дозволяє досягти рівномірного розфарбування. Фурманчук (2006) згадує конкретне застосування такого роду проблеми планування, призначенням університетських курсів на тимчасових інтервалах таким чином, що розподіляє курси рівномірно серед доступних тимчасових інтервалів і дозволяє уникнути планування несумісних пари курсів в той же час.
Теорема Хайнала-Семереді також була використана для пов'язання дисперсії сум випадкових величин з обмеженою залежністю. Якщо кожна змінна залежить від більшості Δ інших, тоді рівномірне розфарбування залежного графу може бути використане для поділу змінних на незалежні підмножини в межах яких може бути застосована нерівність Чернова.
Примітки
- Furmańczyk, (2006).
- Зауважимо, що коли k більше, ніж число вершин у графі, то тоді для рівномірного розфарбування з k кольорами кожен клас кольору містить нуль або одну вершину, отже, кожен граф має межу для рівномірного розфарбування.
- Kierstead, Henry A.; Kostochka, Alexandr V.; Mydlarz, Marcelo; Szemerédi, Endre (17 вересня 2010). A fast algorithm for equitable coloring. Combinatorica 30 (2): 217–224. ISSN 0209-9683. doi:10.1007/s00493-010-2483-5.
References
- Bodlaender, Hans L.; Fomin, Fedor V. (2005). Equitable colorings of bounded treewidth graphs. Theoretical Computer Science 349 (1): 22–30. MR 2183465. doi:10.1016/j.tcs.2005.09.027..
- Bollobás, B.; Eldridge, S. E. (1978). Packings of graphs and applications to computational complexity. Journal of Combinatorial Theory. Series B 25: 105–124. MR 0511983. doi:10.1016/0097-3165(78)90073-0..
- Bollobás, Béla; Guy, Richard K. (1983). Equitable and proportional coloring of trees. Journal of Combinatorial Theory. Series B 34 (2): 177–186. MR 703602. doi:10.1016/0095-8956(83)90017-5..
- Catlin, Paul A. (1974). Subgraphs of graphs. I.. Discrete Math. 10: 225–233. MR 0357230. doi:10.1016/0012-365X(74)90119-8.
- Chen, Bor-Liang; Lih, Ko-Wei (1994). Equitable coloring of trees. Journal of Combinatorial Theory. Series B 61 (1): 83–87. MR 1275266. doi:10.1006/jctb.1994.1032..
- Chen, Bor-Liang; Ko, Ming-Tat; Lih, Ko-Wei (1996). Equitable and m-bounded coloring of split graphs. Combinatorics and Computer Science (Brest, 1995). Lecture Notes in Computer Science 1120. Berlin: Springer-Verlag. с. 1–5. MR 1448914.
- Corrádi, K.; Hajnal, A. (1963). On the maximal number of independent circuits in a graph. Acta Mathematica Academiae Scientiarum Hungaricae 14: 423–439. MR 0200185. doi:10.1007/BF01895727..
- Erdős, Paul (1964). Problem 9. У Fieldler, M. Theory of Graphs and its Applications. Prague: Czech Acad. Sci. Publ. с. 159..
- Fellows, Michael; Fomin, Fedor V.; Lokshtanov, Daniel; Rosamond, Frances; Saurabh, Saket; Szeider, Stefan; Thomassen, Carsten (2007). On the complexity of some colorful problems parameterized by treewidth. Combinatorial optimization and applications. Lecture Notes in Computer Science 4616. Berlin: Springer-Verlag. с. 366–377. MR 2397574. doi:10.1007/978-3-540-73556-4_38..
- Furmańczyk, Hanna (2006). Equitable coloring of graph products. Opuscula Mathematica 26 (1): 31–44. MR 2272280..
- Hajnal, A.; Szemerédi, E. (1970). Proof of a conjecture of P. Erdős. Combinatorial theory and its applications, II (Proc. Colloq., Balatonfüred, 1969). North-Holland. с. 601–623. MR 0297607..
- Janson, Svante; Ruciński, Andrzej (2002). The infamous upper tail. Random Structures &Algorithms 20 (3): 317–342. MR 1900611. doi:10.1002/rsa.10031..
- Kierstead, H. A.; Kostochka, A. V. (2008). A short proof of the Hajnal-Szemerédi theorem on equitable colouring. Combinatorics, Probability and Computing 17 (2): 265–270. MR 2396352. doi:10.1017/S0963548307008619.
- Komlós, János; Sárközy, Gábor N.; Szemerédi, Endre (1998). Proof of the Seymour conjecture for large graphs. Annals of Combinatorics 2 (1): 43–60. MR 1682919. doi:10.1007/BF01626028..
- Meyer, Walter (1973). Equitable coloring. American Mathematical Monthly (Mathematical Association of America) 80 (8): 920–922. JSTOR 2319405. doi:10.2307/2319405..
- Pemmaraju, Sriram V. (2001). Equitable colorings extend Chernoff-Hoeffding bounds. Proc. 12th ACM-SIAM Symp. Discrete Algorithms (SODA 2001). с. 924–925..
- Seymour, P. (1974). Problem section. У McDonough, T. P.; Mavron, Eds., V. C. Combinatorics: Proceedings of the British Combinatorial Conference 1973. Cambridge, UK: Cambridge Univ. Press. с. 201–202..
