Сліпий підпис

Дана ситуація: Боб — нотаріус. Алісі потрібно, щоб він підписав документ, не маючи ніякого уявлення про його зміст. Боб лише завірює, що документ нотаріально засвідчений в зазначений час. Тоді вони діють за таким алгоритмом:

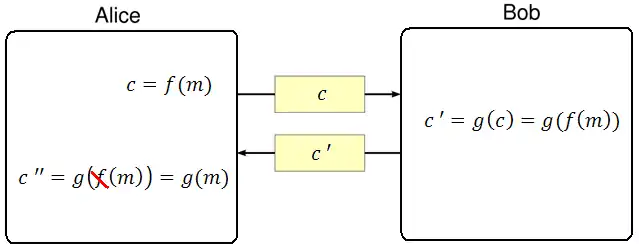
У цій схемі Аліса хоче, щоб Боб наосліп підписав повідомлення ${\displaystyle m}$. Для цього:

1. Аліса зашифровує повідомлення ${\displaystyle m}$ функцією ${\displaystyle f}$., отримуючи зашифроване повідомлення ${\displaystyle c=f(m)}$.
2. Аліса відсилає зашифроване повідомлення Бобу.
3. Боб наосліп (так як не знає, що знаходиться всередині) підписує повідомлення ${\displaystyle c}$ функцією ${\displaystyle g}$, отримуючи ${\displaystyle c^{'}=g(c)=g(f(m))}$.
4. Боб посилає ${\displaystyle c^{'}}$ назад Алісі.
5. Аліса отримує ${\displaystyle c^{'}}$ і прибирає своє шифрування, отримуючи: ${\displaystyle c^{''}=g(f(m))*f^{-1}=g(m)}$.

Цей протокол працює, тільки якщо функції підпису та шифрування комутативні.

1. Боб готує n документів на кожному з яких написано деяке унікальне слово (чим більше n, тим менше у Боба шансів зшахраювати).
2. Боб маскує кожен документ унікальним маскуючим множником і відправляє їх Алісі.
3. Аліса отримує всі документи і випадковим чином вибирає n-1 з них.
4. Аліса просить Боба вислати маскуючі множники для вибраних документів.
5. Боб робить це.
6. Аліса розкриває n-1 документів і переконується, що вони коректні.
7. Аліса підписує останній документ і відсилає Бобу.
8. Тепер у Боба є підписаний Алісою документ з унікальним словом, яке Аліса не знає.

Перша реалізація сліпих підписів була здійснена Чаумом з допомогою криптосистеми RSA:

Припустимо, що спочатку у Боба є відкритий ключ ${\displaystyle }$ , де ${\displaystyle }$ — це модуль, а ${\displaystyle }$ — публічна експонента ключа.

1. Аліса вибирає випадковий маскуючий множник ${\displaystyle r}$ , взаємно простий з ${\displaystyle p}$, і обчислює ${\displaystyle m^{'}\equiv mr^{e}{\bmod {p}}}$.
2. Аліса відсилає ${\displaystyle m^{'}}$ по відкритому каналу Бобу.
3. Боб обчислює ${\displaystyle s^{'}\equiv (m^{'})^{d}{\bmod {p}}}$, використовуючи свій закритий ключ${\displaystyle (p,d)}$.
4. Боб відсилає ${\displaystyle s^{'}}$ назад Алісі.
5. Аліса прибирає своє початкове маскування і отримує підписане Бобом вихідне повідомлення ${\displaystyle m}$ наступним чином: ${\displaystyle s\equiv s^{'}*r^{-1}{\bmod {p}}\equiv m^{d}{\bmod {p}}}$.

Чаум придумав ціле сімейство більш складних алгоритмів сліпого підпису під загальною назвою несподівані сліпі підписи. Їх схеми ще складніше, але вони дають більше можливостей.

Нехай Аліса хоче підписати повідомлення ${\displaystyle }$ у Боба таким чином, щоб, по-перше, Боб не міг ознайомитися з повідомленням в ході підпису, по-друге, щоб Боб не міг згодом при отриманні повідомлення ${\displaystyle }$ і відповідного підпису ідентифікувати користувача, ініціював протокол сліпий підписи для даного конкретного повідомлення (Алісу). Даний протокол реалізується наступним чином:

1. Аліса ініціює взаємодію з Бобом.
2. Боб відправляє Алісі значення ${\displaystyle R=a^{k}\mod p}$.
3. Аліса обчислює значення${\displaystyle R^{'}=Ra^{-w}y^{-t}\mod y}$ (w і t — випадкові числа, що не перевищують ${\displaystyle y}$), ${\displaystyle E^{'}=H(m||R^{'})}$ і ${\displaystyle E=E^{'}+t\mod y}$, після чого відправляє Бобу значення ${\displaystyle E}$ .
4. Боб обчислює значення ${\displaystyle S}$, таке що ${\displaystyle R=a^{S}y^{E}\mod p}$, і відправляє ${\displaystyle S}$ Алісі.
5. Аліса обчислює підпис ${\displaystyle (E^{'},S^{'})}$, де ${\displaystyle E^{'}=E^{-t}\mod y}$ і ${\displaystyle S^{'}=S-w\mod y}$, яка є справжньою по відношенню до повідомлення ${\displaystyle m}$[8].

p — просте число, 510 ≤ |p| ≤ 512 (або 1022 ≤ |p| ≤ 1024), де |p| — розрядність двійкового подання числа p.

q — великий простий дільник числа p-1, 255 ≤ |q| ≤ 256 (або 511 ≤ |q| ≤ 512)

α ≠ 1, α < p, ${\displaystyle }$ mod p = 1.

1. Необхідно згенерувати випадкове k, 1 < k < q;
2. R = (${\displaystyle }$ mod p) mod q — перша частина підпису;
3. H = Hash(m), де Hash — хеш-функція, описана в стандарті ГОСТ Р 34.11-94, m — повідомлення, яке підписується ;
4. S = kH + zR mod q, де z — закритий ключ.
5. Якщо S=0, то повторити операції 1-4.

1. Якщо R < q або S < q, то підпис недійсний. Інакше:
2. R' = (${\displaystyle }$ mod p) mod q, де y — відкритий ключ;
3. Якщо R = R', то підпис дійсний.

Стандарт Білорусії передбачає наступний протокол генерації сліпого підпису до документа M:

1. Необхідно згенерувати випадкове k таке, що 1 < k < q і обчислити ${\displaystyle R=a^{k}}$. Ці дії виконує підписувач. Далі він передає число R користувачеві;
2. Користувач генерує випадкові числа ε і τ такі, що 1 < ε, τ < q і потім обчислює ${\displaystyle R'=R*y^{\tau }*a^{\epsilon }}$, ${\displaystyle E'=F_{H}(R'||M)}$ і E = E' — τ mod q; E — перший елемент підпису — направляється підписувачу;
3. Підписує обчислює другий елемент підпису S = (k — xE) mod q і передає S користувачеві;
4. Користувач обчислює S' = S + ε mod q.

В даному описі використані наступні параметри: q — модуль, за яким ведуться обчислення, просте; a — породжує елемент; x — закритий ключ; y — відкритий ключ[9]..

Нехай ${\displaystyle {\overline {y_{1},y_{s}}}}$ — відкриті ключі, якими володіють s користувачів. Нехай є повідомлення M, яке хочуть підписати m з них. У такому разі всі підписи можна об'єднати в один, довжина якої дорівнює довжині підпису одного користувача і не залежить від m. Це реалізується за правилами наступного протокола:

1. Кожний з m користувачів генерує випадкове число ${\displaystyle t_{\alpha _{j}}}$ < p, де j = ${\displaystyle {\overline {1,m}}}$, p — велике просте число. Далі кожний з m користувачів обчислює ${\displaystyle R_{\alpha _{j}}=(t_{\alpha _{j}})^{k}}$ mod p (k — велика проста ступінь) і розсилає це число всім іншим користувачам даної групи.
2. Кожен користувач обчислює ${\displaystyle R=\prod _{j=1}^{m}R_{\alpha _{j}}}$ mod p. Далі обчислюється e = f(R,M) = RH mod q, де q — велике просте число, відмінне від p, H = Hash(M) — хеш-функція. Число e буде першим елементом колективного підпису.
3. ${\displaystyle S_{\alpha _{j}}=x_{\alpha _{j}}^{e}t_{\alpha _{j}}}$ mod p — частка користувача. Цю частку кожен користувач обчислює і надає іншим.
4. Кожен з користувачів далі обчислює ${\displaystyle S=\prod _{j=1}^{m}S_{\alpha _{j}}}$ mod p. Це другий елемент колективного підпису.

${\displaystyle y=\prod _{j=1}^{m}y_{\alpha _{j}}}$ mod p — колективний відкритий ключ. На його основі відбувається перевірка колективного сліпого підпису за наступним алгоритмом:

1. Обчислюється${\displaystyle R=S^{k}y^{-e}}$ mod p.
2. Обчислюється e' = f(R,M) = RH mod q
3. Якщо e' = e, то підпис дійсний[9].

Найбільш широке застосування протокол сліпих підписів знайшов у сфері цифрових грошей. Наприклад, щоб вкладник не обдурив банк, може використовуватися такий протокол: вкладник пише однаковий номінал купюр на ста документах з різними номерами і депонує в зашифрованому вигляді у банку. Банк вибирає випадковим чином і вимагає розкрити 99 (або n-1) конвертів, переконується, що скрізь написано $10, а не $1000, тоді підписує конверт, що залишився наосліп, не бачачи номера купюри.

Може бути передбачений більш простий варіант: за кожним номіналом купюр у банку закріплена своя пара відкритих ключів. Тоді під підпис надсилається тільки номер купюри, і необхідність перевірки номіналу перед підписом відпадає[1].

Сліпі підписи використовуються для таємного голосування. У протоколі Фуджіока, Окамото і Охта, виборець готує виборчий бюлетень зі своїм вибором, який він зробив, шифрує його секретним ключем, і маскує його. Далі виборець підписує виборчий бюлетень і посилає його валідатору. Валідатор перевіряє, що підпис належить зареєстрованому виборцю, який ще не голосував.

Якщо виборчий бюлетень дійсний, валідатор підписує виборчий бюлетень і повертає його виборцю. Виборець видаляє маскування, розкриваючи таким чином зашифрований виборчий бюлетень, підписаний валідатором. Далі виборець посилає в результаті отриманий підписаний, зашифрований виборчий бюлетень лічильнику, який перевіряє підпис на зашифрованому виборчому бюлетені.

Якщо виборчий бюлетень дійсний, лічильник розміщує його в списку, який буде виданий після всього голосування. Після того, як список виданий, виборці перевіряють, що їх виборчі бюлетені знаходяться в списку і посилають лічильнику ключі розшифрування, необхідні, щоб відкрити їх виборчі бюлетені. Лічильник використовує ці ключі для розшифрування виборчих бюлетенів і додає голос до загального числа. Після виборів лічильник видає ключі розшифрування поряд з зашифрованими виборчими бюлетенями, щоб виборці могли незалежно перевірити вибір[10].