Снарк «Квітка»

Снарк «Квітка» J5
	Снарк «Квітка» J5.
Вершин	20
Ребер	30
Обхват	5
Хроматичне число	3
Хроматичний індекс	4
Властивості	Снарк; Гіпогамільтонів

Снарк «Квітка»
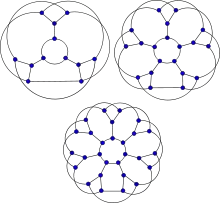	Снарк «Квітка» J3, J5 та J7.
Вершин	4n
Ребер	6n
Обхват	3 для n=3; 5 для n=5; 6 для n≥7
Хроматичне число	3
Хроматичний індекс	4
Властивості	Снарк для n≥5
Позначення	Jn з непарним n

У теорії графів, снарк «Квітка» утворює нескінченне сімейство снарків, відкрите Руфусом Айзексом у 1975 році.[1]

Як і інші снарки, снарк «Квітка» зв'язний кубічний граф без мостів з хроматичним індексом рівним 4. Снарк «Квітка» є негамільтонованим і непланарним. Снарки «Квітка» J₅ and J₇ мають книжкове вкладення 3 та число черг 2.[2]

Побудова

Снарк «Квітка» J_n можна побудувати за допомогою наступного процесу:

Побудуємо n копій зірки з 4 вершинами. Позначимо центральні вершини кожної зірки A_i, а зовнішні вершини B_i, C_i та D_i. Ми отримали незв'язні графи з 4n вершинами та 3n ребрами (A_i – B_i, A_i – C_i та A_i – D_i для 1≤i≤n).
Побудуємо n-цикл (B₁… B_n). Це додає n ребер.
Нарешті побудуємо 2n-цикл (C₁… C_nD₁… D_n). Це додає 2n ребер.

За побудовою, снарк «Квітка» J_n є кубічним графом з 4n вершинами та 6n ребрами. Для того, щоб мати необхідні властивості, значення n має бути непарним.

Особливі випадки

Назва снарк «Квітка» іноді використовується для J₅, який є снарком з 20 вершинами і 30 ребрами.[3] Це один з 6 снарків з 20 вершинами (послідовність A130315 в OEIS). Снарк «Квітка» J₅ є гіпогамільтоновим графом.[4]

J₃ є тривіальною варіацією графу Петерсена, створеного шляхом заміни однієї з його вершин трикутником. Цей граф також відомий як граф Тітце.[5] Для того, щоб уникнути тривіальних випадків, снарки, як правило, обмежені, щоб мати обхват не менше 5. За такого обмеження, J₃ не є снарком.

Галерея

Хроматичне число снарка «Квітка»J₅ 3.
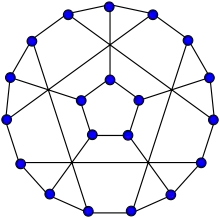
Хроматичний індекс снарка «Квітка» J₅ 4.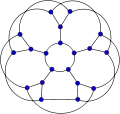
Оригінальне представлення снарка «Квітка» J₅.

Примітки

Isaacs, R. «Infinite Families of Nontrivial Trivalent Graphs Which Are Not Tait Colorable.» Amer. Math. Monthly 82, 221–239, 1975.
Wolz, Jessica; Engineering Linear Layouts with SAT. Master Thesis, University of Tübingen, 2018
Weisstein, Eric W. Flower Snark(англ.) на сайті Wolfram MathWorld.
Weisstein, Eric W. Hypohamiltonian Graph(англ.) на сайті Wolfram MathWorld.
Clark, L.; Entringer, R. (1983). Smallest maximally nonhamiltonian graphs. Periodica Mathematica Hungarica 14 (1): 57–68. doi:10.1007/BF02023582..

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Isaacs, R. «Infinite Families of Nontrivial Trivalent Graphs Which Are Not Tait Colorable.» Amer. Math. Monthly 82, 221–239, 1975.

[2] Wolz, Jessica; Engineering Linear Layouts with SAT. Master Thesis, University of Tübingen, 2018

[3] Weisstein, Eric W. Flower Snark(англ.) на сайті Wolfram MathWorld.

[4] Weisstein, Eric W. Hypohamiltonian Graph(англ.) на сайті Wolfram MathWorld.

[5] Clark, L.; Entringer, R. (1983). Smallest maximally nonhamiltonian graphs. Periodica Mathematica Hungarica 14 (1): 57–68. doi:10.1007/BF02023582..