Снарк (теорія графів)

Снарк в теорії графів — це зв'язний кубічний граф без мостів з хроматичним індексом 4. Іншими словами, це граф з надмірною зв'язністю — усунення будь-якого ребра не призведе до розбиття графу, також кожна вершина має три сусідні вершини і ребра не можна розфарбувати тільки в три кольори, так щоб два ребра одного кольору не сходилися в одній вершині. (З теореми Візінга хроматичний індекс кубічного графу дорівнює 3 або 4.) Щоб уникнути тривіальних випадків, до снарків не відносять графи, які мають обхват менше 5.

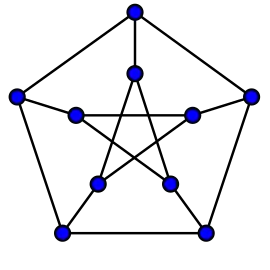
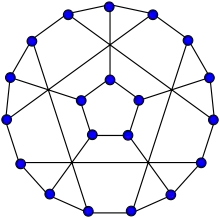
Граф Петерсена є найменшим снарком — всього 10 вершин.
Снарк «Квітка» J5 — один з шести снарків з 20 вершинами.

Вважається, що незважаючи на просте визначення і тривалу історію вивчення, властивості і структура снарка маловідомі.

При вивченні різних важливих і складних проблем теорії графів (таких, як гіпотеза про подвійне покриття циклами і гіпотеза про 5-потік) трапляються цікаві, але в чомусь дивні графи, які називаються снарками. Всупереч своїй простому визначенню … і більш ніж віковому вивченню, їх властивості та структура здебільшого залишаються невідомими.[1]

Оригінальний текст (англ.)
In the study of various important and difficult problems in graph theory (such as the Cycle double cover conjecture and the 5-Flow Conjecture), one encounters an interesting but somewhat mysterious variety of graphs called snarks. In spite of their simple definition...and over a century long investigation, their properties and structure are largely unknown.

Історія
Снарк Секереша

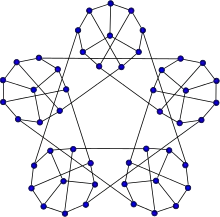
Пітер Тет вперше зацікавився снарками в 1880 році, коли він довів, що теорема про чотири фарби еквівалентна твердженням, що ніякий снарк не є планарним[2]. Першим відомим снарком став граф Петерсена, знайдений в 1898 році. У 1946 році югославський математик Данило Блануша знайшов ще два снарки, обидва з 18 вершинами, що отримали назву Снарк Блануші[3]. Четвертого снарка знайшов двома роками пізніше Татт, який працював під псевдонімом Бланш Декарт (Blanche Descartes), і це був граф порядку 210[4][5] У 1973 році Дьйордь Секереш знайшов п'ятий снарк — Снарк Секереша.[6] У 1975 році Айзекс Руфус узагальнив метод Блануші для побудови двох нескінченних родин снарків — квіти і BDS (снарк Блануші — Декарта — Секереша), сімейство, що включає два снарки Блануші, снарк Декарта і снарк Секереша[7]. Айзекс виявив також снарк з 30 вершинами, що не належить сімейству BDS і не є квіткою — подвійну зірку.

Термін «снарк» увів Мартін Гарднер 1976 року за назвою невловимої істоти «Снарк» з поеми «Полювання на Снарка» Льюїса Керролла[8].

Властивості

Всі снарки є негамільтоновими і більшість з відомих снарків є гіпогамільтоновими — видалення будь-якої окремої вершини дає гамильтонов підграф. Гіпогамільтонові снарки повинні бути бікритичними — видалення будь-яких двох вершин дає підграф, розфарбовуваний реберно в 3 кольори.[9][10]

Було показано, що число снарків для заданого числа вершин обмежена експоненційної функцією[11]. (Будучи кубічними графами, всі снарки повинні мати парне число вершин.) OEIS послідовність A130315 містить число нетривіальних снарків з 2n вершинами для малих значень n[12].

Гіпотеза про подвійне покриття циклами стверджує, що в будь-якому графі без мостів можна знайти набір циклів, що покривають кожне ребро двічі, або, що еквівалентно, що граф можна вкласти в поверхню таким чином, що всі грані будуть простими циклами. Снарки утворюють важкий випадок для цієї гіпотези — якщо вона правильна для снарків, вона правильна для всіх графів[13]. У зв'язку з цим Бранко Ґрюнбаум висловив гіпотезу, що не можна вкласти будь-який снарк в поверхню таким способом, що всі грані є простими циклами і при цьому дві будь-яких межі або не мають загальних ребер, або мають одне спільне ребро. Однак Мартін Кохол знайшов контрприклад до цієї гіпотези Ґрюнбаум[14][15][16].

Теорема про снарки

Татт висловив гіпотезу, що будь-який снарк має граф Петерсена як мінор. Таким чином, він припустив, що найменший снарк, граф Петерсена, можна отримати з будь-якого іншого снарка шляхом стягування деяких ребер і видалення інших. Що еквівалентно (оскільки граф Петерсена має максимальний степінь три) твердженню, що будь-який снарк містить підграф, який можна отримати з графу Петерсена шляхом ділення деяких ребер. Ця гіпотеза є посиленням теореми про чотири фарби, оскільки будь-який граф, що містить граф Петерсена як мінору, не може бути планарним. У 1999 році Робертсон, Сандерс, Сеймур і Томас оголосили про доведення гіпотези[17], однак за станом на 2012 рік доведення так і не опубліковано[18].

Татт також запропонував як гіпотезу узагальнену теорему про снарки для довільних графів — будь-який граф без мостів, що не має графу Петерсена як мінору, має ніде не нульовий 4-потік. Що означає, що ребрам графу можна задати напрямки і позначити числами з множини {1, 2, 3} так, що сума вхідних чисел мінус сума вихідних в кожній вершині ділиться на чотири. Як показав Татт, таке призначення для кубічних графів існує в тому і тільки в тому випадку, коли ребра можна розфарбувати в три кольори, так що в цьому випадку гіпотеза випливає з теореми про снарки. Однак гіпотеза залишається відкритою для інших графів (НЕ кубічних)[19].

Список снарків

Список всіх снарків з 36 вершинами, за винятком снарка з 36 вершинами і обхватом 4, був створений Гуннаром Брінкманном, Яном Гедгебером, Джонасом Хегглундом і Класом Маркстремом в 2012 році[20].

Примітки
  1. Chladný, Miroslav; Škoviera, Martin (2010). Factorisation of snarks. The Electronic Journal of Combinatorics 17: R32.
  2. P. G. Tait. Remarks on the colourings of maps // Proc. R. Soc. Edinburgh. — 1880. — Т. 10. — С. 729.
  3. Danilo Blanuša. Problem četiriju boja // Glasnik Mat. Fiz. Astr. Ser II. — 1946. — Т. 1. — С. 31–42.
  4. Blanche Descartes, Network-colourings, The Mathematical Gazette (London) 32, 67-69, 1948.
  5. Martin Gardner, The Last Recreations: Hydras, Eggs, and Other Mathematical Mystifications, Springer, 2007, ISBN 0-387-25827-2, ISBN 978-0-387-25827-0
  6. G. Szekeres. Polyhedral decompositions of cubic graphs // Bull. Austral. Math. Soc.. — 1973. — Т. 8, вип. 3. — С. 367–387. — DOI:10.1017/S0004972700042660.
  7. R. Isaacs. Infinite families of non-trivial trivalent graphs which are not Tait-colorable // American Mathematical Monthly. — 1975. — Т. 82, вип. 3. — С. 221–239. — DOI:10.2307/2319844. — JSTOR 2319844.
  8. Martin Gardner. Mathematical Games // Scientific American. — 1976. — Т. 4, вип. 234. — С. 126–130.
  9. Steffen E. Classification and characterizations of snarks // Discrete Mathematics. — 1998. — Т. 188, вип. 1–3. — С. 183–203. — DOI:10.1016/S0012-365X(97)00255-0.
  10. Steffen E. On bicritical snarks // Math. Slovaca. — 2001. — Т. 51, вип. 2. — С. 141–150.
  11. Z. Skupień. {{{Заголовок}}}. — Т. 28. — DOI:10.1016/j.endm.2007.01.059.
  12. послідовність A130315 з Онлайн енциклопедії послідовностей цілих чисел, OEIS
  13. F. Jaeger. {{{Заголовок}}}. — Т. 27. — ISBN 978-0-444-87803-8. — DOI:10.1016/S0304-0208(08)72993-1..
  14. Martin Kochol. Journal of Combinatorial Theory, Series B. — 1996. — Т. 67. — С. 34–47.
  15. Martin Kochol. Graph Drawing 2008, Editors: I.G. Tollis, M. Patrignani. — 2009. — Т. 5417. — С. 319–323..
  16. Martin Kochol. Proceedings of the American Mathematical Society. — 2009. — Т. 137. — С. 1613–1619.
  17. Robin Thomas. {{{Заголовок}}}.
  18. Sarah-Marie Belcastro. The continuing saga of snarks // The College Mathematics Journal. — 2012. — Т. 43, вип. 1. — С. 82–87. — DOI:10.4169/college.math.j.43.1.082.. Див. також гіпотезу Хадвігера і результати, пов'язані з розфарбовуванням мінорів графу.
  19. 4-flow conjecture, Open Problem Garden.
  20. Gunnar Brinkmann, Jan Goedgebeur, Jonas Hägglund and Klas Markström. Generation and Properties of Snarks. — 2012.

Посилання
  • Weisstein, Eric W. Snark(англ.) на сайті Wolfram MathWorld.
  • Alen Orbanić, Tomaž Pisanski, Milan Randić, and Brigite Servatius (preprint). «Blanuša Double». Institute for Mathematics, Physics and Mechanics in Ljubljana, Slovenia.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.