Міст (теорія графів)
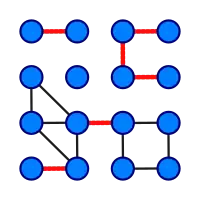
В теорії графів, міст — ребро, видалення якого збільшує кількість компонент зв'язності (або, інакше кажучі, відокремлює підграф)[1]. Рівнозначне визначення, ребро є мостом тоді і тільки тоді, коли вони не є частиною будь-якого циклу.
Подвійне покриття циклами
Графи без мостів породжують цікаву проблему, рішення якої не знайдено досі. Чи вірно, що в будь-якому неорієнтованому графі без мостів існує такий набір циклів, що кожне ребро графу зустрічається в ньому рівно двічі.
Алгоритм знаходження мостів
Перший алгоритм для знаходження мостів в зв'язному графі за лінійний час був віднайдений Робертом Тарджаном в 1974 році[2].
Алгоритм складається з наступних кроків:
- Знайти кістякове дерево для
- Створити дерево з коренем з кістякового дерева
- Обійти дерево в прямому порядку і пронумеровати вершини. Тепер номери батьківських вершин менші за номери нащадків.
- Для кожної вершини при обході у прямому порядку робимо:
- Підраховуємо кількість нащадків для цієї вершини.
- Підраховуємо і
- Для кожної такої, що : якщо і , тоді ребро буде мостом.
Визначення: Ребро поза деревом між і позначається . Ребро в дереві з батьківською позначається .
де батьківська вершина для .
кількість нащадків v (включно із собою) в кістяковому дереві.
і позначки вершин з найменшою і найбільшою позначкою обходу прямого порядку, досяжних з проходом по піддереву з коренем у , разом з щонайбільше одним ребром не в дереві.
Ребро є мостом тоді і тільки тоді, коли з піддерева з коренем у неможливо потрапити у вершину, яка не є нащадком . Це легко перевірити, бо піддерево з коренем у (об'єднує всіх нащадків w) містить наступні вершини , тож ми можемо просто перевірити, знаходяться в цій множині чи ні для перевірки чи є ребро мостом.
Примітки
- Кормен, Томас; Лейзерсон, Чарльз; Рівест, Рональд; Стайн, Кліфорд (2019). Розділ 22: Елементарні алгоритми на графах. Вступ до алгоритмів (вид. 3). К.І.С. с. 633. ISBN 978-617-684-239-2.
- Tarjan, R. Endre (1974). A note on finding the bridges of a graph. Information Processing Letters 2 (6): 160–161. MR 0349483. doi:10.1016/0020-0190(74)90003-9..
