Степінь Тюрінга

Концепція степені Тюрінга є фундаментальною в теорії обчислюваності, де множини натуральних чисел зазвичай розглядаються як проблеми вибору. Степінь Тюрінга для даної множини є мірою того, наскільки важко розв'язати проблему вибору, пов'язану з множиною, тобто визначити, чи є довільне число у заданій множині.

Дві множини еквівалентні за Тюрінгом, якщо вони мають однаковий рівень нерозв'язності; кожна степінь Тюрінга є колекцією множин, еквівалентних за Тюрінгом, тож дві множини мають різні степені Тюрінга тільки тоді, коли вони не еквівалентні за Тюрінгом. Більше того, степені Тюрінга є частково впорядкованими, тож якщо степінь Тюрінга для множини X менша за степінь Тюрінга для множини Y, тоді будь-яка (необчислювана) процедура, що правильно визначає чи належить число множині Y може бути ефективно перетворена на процедуру, що вирішує, чи належить число множині X. У цьому сенсі степінь Тюрінга множини відповідає рівню її нерозв'язності.

Термін степінь Тюрінга був введений Емілем Постом (1944). Багато фундаментальних результатів у цій сфері були встановлені Стівеном Коулом Кліні та Постом (1954). Степінь Тюрінга з тих пір є областю інтенсивних наукових досліджень. Багато доведень у цій області використовують метод доведення, відомий як метод пріоритету.

Тут і нижче під терміном множина будемо розуміти множину натуральних чисел. Множина X є редукція Тюрінга для множини Y, якщо існує пророча машина Тюрінга, котра приймає рішення щодо належності до X, коли є пророцтво щодо членства у Y. Позначення X ≤_T Y означає, що X скорочується за Тюрінгом до Y.

Дві множини X та Y є еквівалентними за Тюрінгом, якщо X скорочується за Тюрінгом до Y, а Y скорочується за Тюрінгом до X. Позначання X ≡_T Y означає, що X та Y є еквівалентними за Тюрінгом. Відношення ≡_T може бути розглянуто як відношення еквівалентності, що означає, що для кожної множини X, Y та Z:

• X ≡_T X
• X ≡_T Y означає, що Y ≡_T X
• Якщо X ≡_T Y таY ≡_T Z, тоді X ≡_T Z.

Степінь Тюрінга це клас еквівалентності відношення ≡_T. Позначення [X] означає, що клас еквівалентності містить множину X. Повна колекція степенів Тюрінга позначається як ${\displaystyle {\mathcal {D}}}$.

Степені Тюрінга частково впорядковані ≤ це означає, що [X] ≤ [Y] тоді і тільки тоді, коли X ≤_T Y. Існує унікальна степінь Тюрінга, яка містить всі обчислювані множини, і ця степінь менша, ніж будь-яка інша степінь. Вона позначається як 0 (нуль), тому що це найменший елемент частково впорядкованої множини ${\displaystyle {\mathcal {D}}}$. (Часто для позначення степені Тюрінга використовують жирний шрифт, аби відрізнити їх від множин. Коли ніякої плутанини не може статись, як наприклад з [X], жирний шрифт не є необхідним.)

Для двох будь-яких множин X та Y, X об'єднане з Y, пишеться як X ⊕ Y, є за визначенням об'єднанням множин {2n : n ∈ X} та {2m+1 : m ∈ Y}. Степінь Тюрінга для об'єднання X ⊕ Y є найменшою верхньою гранню степенів X та Y. Так ${\displaystyle {\mathcal {D}}}$ є об'єднанням-напівграткою. Найменша верхня грань ступенів a та b позначається як a ∪ b. Відомо, що ${\displaystyle {\mathcal {D}}}$ не є решіткою, адже там існує пари ступенів без найбільшої нижньої грані.

Для будь-якої множини X позначення X′ означає множину індексів для пророчої машини, на котрих відбудеться зупинка при використанні X як пророцтва. Множина X′ називається оператором стрибку Тюрінга для X. Оператор стрибку Тюрінга для степені [X] є, за визначенням, степінь [X′]; це є валідним визначенням, тому що X′ ≡_T Y′ для X ≡_T Y. Ключовим прикладом є 0′, степінь для проблеми зупинки.

• Кожна степінь Тюрінга є зліченною множиною, так як вона містить рівно ${\displaystyle \aleph _{0}}$ множин.
• Існує ${\displaystyle 2^{\aleph _{0}}}$ степенів Тюрінга.
• Для кожного степеня a виконується чітка нерівність a < a′.
• Для кожного степеня a, множина степенів нижче a є зліченною. Множина степенів більних за a має розмір ${\displaystyle 2^{\aleph _{0}}}$.

Багато досліджень було присвячено структурі степенів Тюринга. Наступний список містить лише деякі з багатьох відомих результатів. Один загальний висновок, який можна зробити з досліджень, полягає в тому, що структура степенів Тюринга надзвичайно складна.

Степінь називається р.п. (рекурсивно перераховним), якщо він містить рекурсивно перераховну множину. Кожний р.п. степінь менший або рівний до 0′, але не кожен степінь, менший за 0′, є р.п. степенем.

• (G. E. Sacks, 1964) Р.П степені є щільними; між двома р.п. степенями існує третій р.п. степінь.
• (A. H. Lachlan, 1966a and C. E. M. Yates, 1966) Існує два р.п. степеня без найбільшої нижньої грані в р.п. степенях.
• (A. H. Lachlan, 1966a and C. E. M. Yates, 1966) Існує пара ненульових р.п. степенів з найбільшою нижньою граню рівною 0.
• (S. K. Thomason, 1971) Кожна скінченна розподілена решітка може міститися в р.п. степені. Фактично, перераховна булева алгебра може міститися таким чином, що зберігатиметься супремум та інфімум.
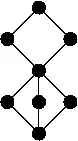
• (A. H. Lachlan and R. I. Soare, 1980) Не всі скінченні решітки можуть міститися в р.п. степенях (таким чином, аби зберігався супремум та інфімум). Наступна решітка не може міститися в р.п. степені:

• (A. H. Lachlan, 1966b) TНе існує пари р.п. степенів, чиї найбільші нижні грані дорівнюють 0, а найменші верхні грані дорівнюють 0′. Цей результат неформально називається недіамантова теорема.
• (L. A. Harrington та T. A. Slaman, див. Nies, Shore, та Slaman (1998)) Теорема першого порядку для р.п. степенів мовою ⟨ 0, ≤, = ⟩ є багатозначною еквівалентністю до теорії справжнього першого порядку арифметики.

Еміль Пост вивчав р.п. степінь Тюрінга і задався питанням, чи є якийсь р.п. степінь точно між 0 та 0′. Проблема побудови такого степеня (або доведення, що такого не існує) стала називатися проблемою Поста. Ця проблема була вирішена незалежно Фридбергом та Мучником у 1950-х роках. Було доведено, що ці проміжниі р.п. степені існують. Обидва їх докази використовували один і той самий новий метод побудови р.п. степенів, який отримав назву метод пріоритету. Метод пріоритету зараз є основною технікою для встановлення результатів стосовно р.п. множин.

Ідея методу пріоритету для побудови р.п. множини X полягає у переліку зліченої послідовності вимог, які X повинна задовольняти. Наприклад, щоб побудувати р.п. множину X між 0 та 0′, досить задовольнити вимогам A_e і B_e для кожного натурального числа e, де A_e вимагає, щоб пророча машина з індексом e не обчислювала 0′ з X і B_e вимагає, щоб машина Тюрінга з індексом e (і без пророцтва) не обчислювала X. Ці вимоги вводяться в пріоритетний порядок, що є явною бієкцією вимог та натуральних чисел. Доведення проходить індуктивно з одним етапом для кожного натурального числа; ці етапи можна розглядати як етапи часу, протягом яких перелічується набір X. На кожному етапі числа можуть бути або введені в X, або назавжди відхилені від вводу у X задля спроби задовольнити вимоги (тобто змусити їх триматись, коли всі X перераховано). Іноді, число можна перерахувати в X, щоб задовольнити одну вимогу, але це може призвести до того, що раніше задоволена вимога стає незадоволеною (тобто вражена). Пріоритетний порядок на вимоги використовується для визначення того, яку вимогу потрібно виконати у цьому випадку. Неформальна ідея полягає в тому, що, якщо вимога вражена, то вона в кінцевому підсумку припинить бути такою після того, як всі вимоги щодо вищого пріоритету перестануть бути враженими, хоча не кожний пріоритетний аргумент має таку властивість. Потрібно зробити зауваження, що загальна множина X є р.п. і задовольняє всім вимогам. Пріоритетні аргументи можуть бути використані для доведення багатьох фактів про р.п. множини; використовувані вимоги та спосіб, яким вони виконуються, повинні бути ретельно відібрані для отримання необхідного результату.

• Martin measure

Монографії (рівень бакалавра)

• Cooper, S.B. Computability theory. Chapman & Hall/CRC, Boca Raton, FL, 2004. ISBN 1-58488-237-9
• Cutland, N. Computability. Cambridge University Press, Cambridge-New York, 1980. ISBN 0-521-22384-9; ISBN 0-521-29465-7

Монографії та дослідницькі роботи (рівень магістра)

• Ambos-Spies, K. and Fejer, P. Degrees of Unsolvability. Unpublished. http://www.cs.umb.edu/~fejer/articles/History_of_Degrees.pdf
• Lerman, M. Degrees of unsolvability. Perspectives in Mathematical Logic. Springer-Verlag, Berlin, 1983. ISBN 3-540-12155-2
• Odifreddi, P. G. (1989). Classical Recursion Theory. Studies in Logic and the Foundations of Mathematics 125. Amsterdam: North-Holland. ISBN 978-0-444-87295-1. MR 982269.
• Odifreddi, P. G. (1999). Classical recursion theory. Vol. II. Studies in Logic and the Foundations of Mathematics 143. Amsterdam: North-Holland. ISBN 978-0-444-50205-6. MR 1718169.
• Rogers, H. The Theory of Recursive Functions and Effective Computability, MIT Press. ISBN 0-262-68052-1, ISBN 0-07-053522-1
• Sacks, Gerald E. Degrees of Unsolvability (Annals of Mathematics Studies), Princeton University Press. ISBN 978-0-6910-7941-7
• Simpson, S. Degrees of unsolvability: a survey of results. Handbook of Mathematical Logic, North-Holland, 1977, pp. 631–652.
• Shoenfield, Joseph R. Degrees of Unsolvability, North-Holland/Elsevier, ISBN 978-0-7204-2061-6.
• Shore, R. (1993). The theories of the T, tt, and wtt r.e. degrees: undecidability and beyond. У Univ. Nac. del Sur, Bahía Blanca. Proceedings of the IX Latin American Symposium on Mathematical Logic, Part 1 (Bahía Blanca, 1992). Notas Lógica Mat. 38. с. 61–70.
• Soare, R. Recursively enumerable sets and degrees. Perspectives in Mathematical Logic. Springer-Verlag, Berlin, 1987. ISBN 3-540-15299-7
• Soare, Robert I. Recursively enumerable sets and degrees. Bull. Amer. Math. Soc. 84 (1978), no. 6, 1149–1181. MR508451

Науково-дослідницькі роботи

• Kleene, Stephen Cole; Post, Emil L. (1954). The upper semi-lattice of degrees of recursive unsolvability. Annals of Mathematics. Second Series 59 (3): 379–407. ISSN 0003-486X. JSTOR 1969708. MR 0061078. doi:10.2307/1969708.
• Lachlan, A.H. (1966a). Lower Bounds for Pairs of Recursively Enumerable Degrees. Proceedings of the London Mathematical Society 3 (1): 537. doi:10.1112/plms/s3-16.1.537.
• Lachlan, A.H. (1966b). The impossibility of finding relative complements for recursively enumerable degrees. J. Symb. Logic 31 (3): 434–454. JSTOR 2270459. doi:10.2307/2270459.
• Lachlan, A.H.; Soare, R.I. (1980). Not every finite lattice is embeddable in the recursively enumerable degrees. Advances in Mathematics 37: 78–82. doi:10.1016/0001-8708(80)90027-4.
• Nies, André; Shore, Richard A.; Slaman, Theodore A. (1998). Interpretability and definability in the recursively enumerable degrees. Proceedings of the London Mathematical Society 77 (2): 241–291. ISSN 0024-6115. MR 1635141. doi:10.1112/S002461159800046X.
• Post, Emil L. (1944). Recursively enumerable sets of positive integers and their decision problems. Bulletin of the American Mathematical Society 50 (5): 284–316. ISSN 0002-9904. MR 0010514. doi:10.1090/S0002-9904-1944-08111-1.
• Sacks, G.E. (1964). The recursively enumerable degrees are dense. Annals of Mathematics. Second Series 80 (2): 300–312. JSTOR 1970393. doi:10.2307/1970393.
• Shore, Richard A.; Slaman, Theodore A. (1999). Defining the Turing jump. Mathematical Research Letters 6: 711–722. ISSN 1073-2780. MR 1739227. doi:10.4310/mrl.1999.v6.n6.a10.
• Simpson, Stephen G. (1977). First-order theory of the degrees of recursive unsolvability. Annals of Mathematics. Second Series 105 (1): 121–139. ISSN 0003-486X. JSTOR 1971028. MR 0432435. doi:10.2307/1971028.
• Thomason, S.K. (1971). Sublattices of the recursively enumerable degrees. Z. Math. Logik Grundlag. Math. 17: 273–280. doi:10.1002/malq.19710170131.
• Yates, C.E.M. (1966). A minimal pair of recursively enumerable degrees. Journal of Symbolic Logic 31 (2): 159–168. JSTOR 2269807. doi:10.2307/2269807.