Субдиференціал
У математиці, зокрема, в опуклому аналізі, поняття субдиференціалу та субградієнту є узагальненнями відповідних понять диференціалу та градієнту класичного аналізу.
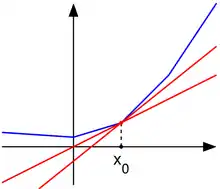
Опукла функція (синя) та «лінії субградієнту» в x0 (червоні).
Визначення
Нехай — функція на евклідовому просторі Вектор називається субградієнтом функції в точці якщо справджується нерівність
Множина всіх субградієнтів називається субдиференціалом функції f(x) в точці і позначається . Використовуючи математичну символіку можна записати визначення субдиференціалу:
Властивості
- Опукла функція є диференційовною в точці тоді і тільки тоді, коли субдиференційал функції в точці складається з єдиного числа. Це число і є похідною функції в точці .
- Точка є точкою глобального мінімуму опуклої функції тоді і тільки тоді, коли нуль входить до її субдиференціалу, тобто коли на рисунку вище можна провести горизонтальну дотичну в точці до графіку функції .
- Якщо і є опуклими функціями з субдиференціалами і , то субдиференціалом функції є , де позначає суму Мінковського.
Див. також
Джерела
- Моклячук М.П. Основи опуклого аналізу. К.:ТвіМС, 2004. – 240с.
- М.П.Моклячук, Негладкий аналіз та оптимізація
- J.M. Borwein, A.S. Lewis (2000). Convex Analysis and Nonlinear Optimization. Springer, New York.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.
