Сума Мінковського

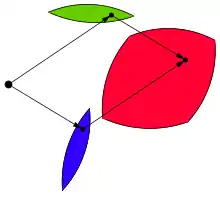
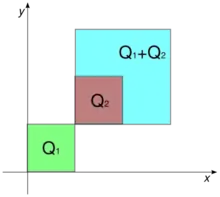
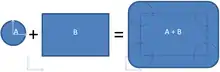
В геометрії, Сумою Мінковського (англ. minkowski sum) двох множин радіус-векторів A і B у евклідовому просторі утворюється додаванням кожного вектора з A до кожного вектора з B, тобто множина

A+B=\{\mathbf {a} +\mathbf {b} \mid \mathbf {a} \in A,\ \mathbf {b} \in B\}.

Сума Мінковського $A + B$
B
A

Червона фігура є сумою синьої та зеленої фігур

Приклад

В опуклій оболонці червоної множини, кожна синя точка є опуклою комбінацією якихось червоних точок

Сума Мінковського двох квадратів Q₁=

[0,1]

² і Q₂=

[1,2]

² це квадратQ₁+Q₂=

[1,3]

².

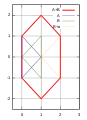
Наприклад, якщо ми маємо дві множини A і B, кожна з трьох радіус-векторів (неформально, трьох точок), що представляють вершини двох трикутників у $\mathbb {R} ^{2}$ , з координатами

A = {(1, 0), (0, 1), (0, -1)}

і

B = {(0, 0), (1, 1), (1, -1)}

,

тоді сума Мінковського є
$A + B = {(1, 0)$ , $(2, 1)$ , $(2, -1)$ , $(0, 1)$ , $(1, 2)$ , $(1, 0)$ , $(0, -1)$ , $(1, 0)$ , $(1, -2)}$ , яка виглядає як шестикутник, з трьома точками, що повторюються в $(1, 0)$ .

Для додавання Мінковського, нульова множина {0}, що містить лише нульовий вектор 0, є нейтральним елементом: Для будь-якої підмножини S, векторного простору

S + {0} = S;

Порожня множина важлива для додавання Мінковського, бо вона знищує будь-яку іншу підмножину: для будь-якої підмножини, S, векторного простору, його сума з порожньою множиною — порожня множина: $\emptyset$ .

Прочісування одного опуклого об'єкту іншим

Алгоритм для опуклих многокутників

Кут між вектором

{\overline {pq}}

та віссю

x.

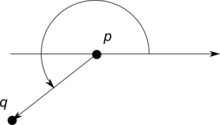
В алгоритмі ми використовуємо поняття кута між вектором ${\overline {pq}}$ та віссю $x.$

Алгоритм СУМА_МІНКОВСЬКОГО $({\mathcal {P}},{\mathcal {R}})$ Вхід. Опуклий многокутник ${\mathcal {P}}$ з вершинами $v_{1},\cdot ,v_{n},$ і опуклий многокутник ${\mathcal {R}}$ з вершинами $w_{1},\cdots ,w_{m}.$ Списки вершин повинні бути впорядковані проти годинникової стрілки, а $v_{1},w_{1}$ повинні мати найменші $y$ -координати (і найменші $x$ -координати у випадку кількох вершин з найменшою $y$ -координатою). Вихід. Сума Мінковського ${\mathcal {P}}\oplus {\mathcal {R}}$ . $i\leftarrow 1;j\leftarrow 1$ $v_{n+1}\leftarrow v_{1};v_{n+2}\leftarrow v_{2};w_{m+1}\leftarrow w_{1};w_{m+2}\leftarrow w_{2}$ повторювати Додати $v_{i}+w_{j}$ як вершину у ${\mathcal {P}}\oplus {\mathcal {R}}$ . якщо $\angle (v_{i}v_{i+1})<\angle (w_{j}w_{j+1})$ тоді $i\leftarrow (i+1)$ інакше якщо $\angle (v_{i}v_{i+1})>\angle (w_{j}w{j+1})$ тоді $j\leftarrow (j+1)$ інакше $i\leftarrow (i+1);j\leftarrow (j+1)$ допоки $(i=n+1$ та $j=m+1)$

Алгоритм виконується за лінійний час.

Обчислення суми Мінковського для неопуклих многокутників не дуже складне: тріангулювати обидва многокутники, обчислити суму Мінковського для кожної двійки трикутників і об'єднати їх.

Теорема: Нехай ${\mathcal {P,R}}-$ многокутники з $n,m$ вершинами відповідно. Складність суми Мінковського ${\mathcal {P}}\oplus {\mathcal {R}}$ має такі границі:

це $O(n+m)$ якщо обидва многокутники опуклі;
це $O(nm)$ якщо один з многокутників опуклий і один неопуклий;
це $O(n^{2}m^{2})$ якщо обидва многокутники неопуклі.

Ці границі тугі в найгіршому випадку.

Посилання

Hazewinkel, Michiel, ред. (2001). Сума Мінковського. Encyclopedia of Mathematics. Springer. ISBN 978-1-55608-010-4.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.