Теорема Каратеодорі про опуклу оболонку

Теорема Каратеодорі, відноситься до опуклої геометрії та стверджує, що якщо точка x з R^d лежить в опуклій оболонці множини P, то для P знайдеться підмножина P′, яка складається з d + 1 або меншої кількості точок, таких що x лежить в опуклій оболонці P′. Це рівнозначно тому, що x лежить в r-симплексі з вершинами в множині P, де ${\displaystyle r\leqslant d}$. Теорема названа на честь Костянтина Каратеодорі, який її довів в 1911 році у випадку, коли P — компактна множина. У 1914 році Ернст Стейніц розповсюдив теорему Каратеодорі на випадок довільної множини P з R^d.

Ілюстрація теореми Каратеодорі для квадрата в R²

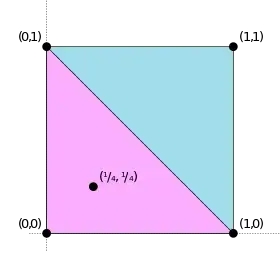
Наприклад, розглянемо набір P = {(0,0), (0,1), (1,0), (1,1)}, який є підмножиною в R². Опукла оболонка цієї множини являє собою квадрат. Розглянемо тепер точку x = (1/4, 1/4), яка знаходиться в опуклій оболонці P. Тоді можна побудувати множину {(0,0), (0,1), (1,0)} = P′, опукла оболонка якої є трикутник і охоплює x, і, отже, теорема виконується в даному випадку, так як потужність |P′| = 3. Ілюстрація теореми Каратеодорі в 2 вимірному випадку, полягає в тому, що можна побудувати трикутник, що складається з точок з P, який охоплює будь-яку точку P.