Теорема Петерсена

У математичній дисципліні теорії графів, теорема Петерсена, названа на честь Юліуса Петерсена, є одним з найбільш ранніх результатів в теорії графів і може бути сформульована таким чином:

Теорема Петерсена. Кожен кубічний граф, який не містить мостів має ідеальне парування.[1]

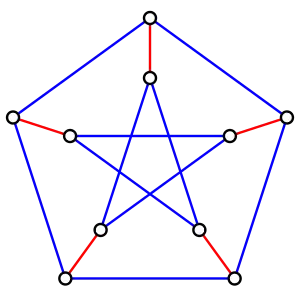
Ідеальне парування (червоні ребра), в графі Петерсена. Оскільки граф Петерсена кубічний і в ньому відсутні мости, він задовольняє умовам теореми Петерсона.

Кубічний (але з мостами) граф з неідеальною відповідністю, демонструє, що умова відсутності мостів в теоремі Петерсена є необхідною.

Іншими словами, якщо граф має рівно три ребра в кожній вершині, і кожне ребро належить до циклу, то він має набір ребер, який торкається кожної вершини рівно один раз.

Доведення

Ми показуємо, що для кожного кубічного графу який не містить мостів $G = (V, E)$ ми маємо, що для кожного набору $U \subseteq V$ кількість компонентів зв'язності в графі, індукованість $V - U$ з непарним числом вершин, не перевищує потужності $U$ . Тоді як згідно з теоремою Татта $G$ містить ідеальну відповідність.

Нехай $G i$ буде компонентом з непарним числом вершин в графі, який індукований набором вершин $V - U$ . Нехай $V i$ позначає вершини $G i$ і нехай $m i$ позначає кількість ребер $G$ з одною вершиною в $V i$ та одною в $U$ . Простим подвійним підрахунком аргументів, маємо, що

\sum \nolimits _{v\in V_{i}}\deg _{G}(v)=2|E_{i}|+m_{i},

де $E i$ — набір ребер $G i$ з обома вершинами в $V i$ . З огляду на те, що

\sum \nolimits _{v\in V_{i}}\deg _{G}(v)=3|V_{i}|

є непарним числом, і $2| E i |$ — парне число, отже, $m i$ повинно бути непарним числом. Більш того, так як $G$ не містить мостів, то $m i \geq 3$ .

Нехай $m$ буде кількістю ребер у $G$ з одною вершиною у $U$ та одною вершиною в графі, який індукований $V - U$ . Кожен компонент з непарним числом вершин вносить, принаймні 3 ребра до $m$ , і вони є унікальними, отже, число таких компонентів становить не більше $m /3$ . У гіршому випадку, кожне ребро з однією вершиною в $U$ входить до $m$ , і таким чином $m \leq 3| U |$ . Ми отримуємо

|U|\geq {\frac {1}{3}}m\geq |\{{\text{компоненти з непарною кількістю вершин}}\}|,

що показує, що умова теореми Татта зберігається.

Історія

Теорема належить Юліусу Петерсену, датському математику. Її можна розглядати як один з перших результатів в теорії графів. Теорема з'являється вперше в 1891 році у статті «Die Theorie der regulären graphs».[1] За сьогоднішніми мірками доказ Петерсена цієї теореми складний. Ряд спрощень його доказу завершилися в доказах Frink, (1926) та König, (1936).

У сучасних підручниках теорема Петерсена розглядається як додаток до теореми Татта.

Додатки

У кубічному графі з ідеальним паруванням, ребра, які не є в ідеальному паруванні утворюють 2-фактор. При орієнтуванні 2-фактору, ребра з ідеальним паруванням можуть бути розширені до шляху довжини три, скажімо, приймаючи зовнішньо-орієнтовані ребра. Це показує, що кожен кубічний граф, який не містить мостів, розпадається на крайові непересічні шляхи довжини три.[2]
Теорема Петерсена також може бути застосована, щоб показати, що кожен планарний граф можна розкласти на безліч крайових непересічних шляхів довжини три. В цьому випадку, двоїстий граф є кубічним і не містить мостів, тому по теоремі Петерсена він має відповідність, що відповідає до спаровування суміжних граней трикутника в вихідному графі . Кожна пара трикутників дає шлях довжини три, який містить ребро, яке з'єднує трикутники разом з двома із чотирьох лишившихся ребер.[3]
Застосовуючи теорему Петерсена до двоїстого графу сітки з трикутників і з'єднуючи пари трикутників, що не поєднані, можна розкласти сітку в циклічну смугу з трикутників. З деяких подальших перетворень вона може бути перетворена в одну смугу, і, отже, дає спосіб для перетворення сітки з трикутників таким чином, що його двоїстий граф стає гамільтоновим шляхом.[4]

Розширення

Кількість ідеальних парувань в кубічному графі, який не містить мостів

Ласло Ловасом і Майклом Пламмером було висловлено припущення, що кількість ідеальних парувань, які містяться в кубічному графі без мостів — єекспоненціальною щодо кількості вершин графу $n$ .[5] Гіпотеза була вперше доведена для двочасткового, кубічного графу, що не містить мостів Voorhoeve, (1979), пізніше для планарного, кубічного графу, що не містить мостів Chudnovsky та Seymour, (2012). Загальний випадок був вирішений Esperet та ін., (2011), коли було показано, що кожен кубічний граф, що не містить мостів, містить принаймні $2^{n/3656}$ ідеальних парувань.

Алгоритмічна версія

Biedl та ін., (2001) обговорює ефективні варіанти теореми Петерсена. На підставі доведення Фрінка[6] вони отримують $O (n log 4 n)$ алгоритм для обчислення ідеальних парувань в кубічному графі, що не містить мостів з $n$ вершинами. Якщо граф, ще і планарний, то та ж стаття приводить алгоритм, який має швидкість $O (n)$ . Їх час оцінки $O (n log 4 n)$ , може бути покращено на основі наступних удосконалень часу для підтримки набору мостів в динамічному графі.[7] Подальше скорочення часу до $O (n log 2 n)$ або (з додатковими випадковими структурами даних) до $O (n log n (log log n) 3)$ , було отримане Diks та Stanczyk, (2010).

Вищий ступінь

Якщо G є регулярним графом ступеня d, чия реберна зв'язність принаймні d − 1, та G має парне число вершин, то він має ідеальне парування. Більш того, кожне ребро G належить, що найменш, до одного ідеального парування. Умова на число вершин може бути опущена з цього результату, коли ступінь непарний, тому, що в цьому випадку (згідно з лемою про рукостискання) число вершин завжди парне.[8]

Замітки

Petersen, (1891).
Див. для прикладу Bouchet та Fouquet, (1983).
Häggkvist та Johansson, (2004).
Meenakshisundaram та Eppstein, (2004).
Lovász та Plummer, (1986).
Frink, (1926).
Thorup, (2000).
Naddef та Pulleyblank, (1981), Theorem 4, p. 285.

Посилання

Biedl, Therese C.; Bose, Prosenjit; Demaine, Erik D.; Lubiw, Anna (2001). Efficient algorithms for Petersen's matching theorem. Journal of Algorithms 38 (1): 110–134. MR 1810434. doi:10.1006/jagm.2000.1132.
Bouchet, André; Fouquet, Jean-Luc (1983). Trois types de décompositions d'un graphe en chaînes. У C. Berge, P. Camion, D. Bresson; Sterboul, F. Combinatorial Mathematics: Proceedings of the International Colloquium on Graph Theory and Combinatorics (Marseille-Luminy, 1981). North-Holland Mathematics Studies (French) 75. North-Holland. с. 131–141. MR 0841287. doi:10.1016/S0304-0208(08)73380-2.
Chudnovsky, Maria; Seymour, Paul (2012). Perfect matchings in planar cubic graphs. Combinatorica 32 (4): 403–424. MR 2965284. doi:10.1007/s00493-012-2660-9.
Diks, Krzysztof; Stanczyk, Piotr (2010). Perfect matching for biconnected cubic graphs in $O(n log 2 n)$ time. У van Leeuwen, Jan; Muscholl, Anca; Peleg, David; Pokorný, Jaroslav; Rumpe, Bernhard. SOFSEM 2010: 36th Conference on Current Trends in Theory and Practice of Computer Science, Špindlerův Mlýn, Czech Republic, January 23–29, 2010, Proceedings. Lecture Notes in Computer Science 5901. Springer. с. 321–333. doi:10.1007/978-3-642-11266-9_27.
Esperet, Louis; Kardoš, František; King, Andrew D.; Králʼ, Daniel; Norine, Serguei (2011). Exponentially many perfect matchings in cubic graphs. Advances in Mathematics 227 (4): 1646–1664. MR 2799808. doi:10.1016/j.aim.2011.03.015.
Frink, Orrin (1926). A proof of Petersen’s theorem. Annals of Mathematics. Second Series 27 (4): 491–493. doi:10.2307/1967699.
Häggkvist, Roland; Johansson, Robert (2004). A note on edge-decompositions of planar graphs. Discrete Mathematics 283 (1–3): 263–266. MR 2061501. doi:10.1016/j.disc.2003.11.017.
König, Dénes (1936). Theorie der endlichen und unendlichen Graphen; kombinatorische Topologie der Streckenkomplexe.
Lovász, László; Plummer, M. D. (1986). Matching Theory. Annals of Discrete Mathematics 29. North-Holland. ISBN 0-444-87916-1. MR 0859549.
Meenakshisundaram, Gopi; Eppstein, David (2004). Single-strip triangulation of manifolds with arbitrary topology. Proc. 25th Conf. Eur. Assoc. for Computer Graphics (Eurographics '04). Computer Graphics Forum 23. с. 371–379. arXiv:cs.CG/0405036. doi:10.1111/j.1467-8659.2004.00768.x.
Naddef, D.; Pulleyblank, W. R. (1981). Matchings in regular graphs. Discrete Mathematics 34 (3): 283–291. MR 613406. doi:10.1016/0012-365X(81)90006-6..
Petersen, Julius (1891). Die Theorie der regulären graphs. Acta Mathematica 15: 193–220. doi:10.1007/BF02392606.
Thorup, Mikkel (2000). Near-optimal fully-dynamic graph connectivity. Proc. 32nd ACM Symposium on Theory of Computing. с. 343–350. ISBN 1-58113-184-4. MR 2114549. doi:10.1145/335305.335345.
Voorhoeve, Marc (1979). A lower bound for the permanents of certain (0,1)-matrices. Indagationes Mathematicae 82 (1): 83–86. MR 0528221. doi:10.1016/1385-7258(79)90012-X.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[p1891-1] Petersen, (1891).

[2] Див. для прикладу Bouchet та Fouquet, (1983).

[3] Häggkvist та Johansson, (2004).

[4] Meenakshisundaram та Eppstein, (2004).

[5] Lovász та Plummer, (1986).

[6] Frink, (1926).

[FOOTNOTEThorup2000-7] Thorup, (2000).

[8] Naddef та Pulleyblank, (1981), Theorem 4, p. 285.