Теорема Радона
В геометрії, теорема Радона на опуклих множинах, опублікована Йоганом Радоном у 1921, стверджує, що будь-яку множину з d + 2 точок в Rd можна розбити на дві неперетинні множини, чиї опуклі оболонки перетинаються. Точка, що належить перетину цих опуклих оболонок, називається точка Радона множини.
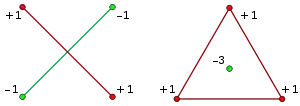
Наприклад, у цьому випадку d = 2, будь-яка множина з чотирьох точок на Евклідовій площині розбивна одним з двох способів. Вона може утворити трійку і одинака, де опукла оболонка трійки містить одинака; або ж, вона може утворити дві пари точок, так що ці точки формують кінці відрізків, що перетинаються.
Доведення і побудова
Розглянемо довільну множину з d + 2 точок в d-вимірному просторі. Тоді існує множина множників a1, ..., ad + 2, не всі з яких рівні нулю, що розв'язує систему лінійних рівнянь
з того, що маємо d + 2 невідомих (множники), але лише d + 1 рівнянь, яким вони мають задовольняти (одна для кожної координати і кінцеве рівняння, що накладає умову на суму множників). Оберемо якийсь ненульовий розв'язок a1, ..., ad + 2. Нехай I буде множиною точок з додатними множниками і нехай J буде множиною точок з від'ємними множниками або нулем. Тоді I і J утворюють необхідний розподіл точок на дві підмножини, опуклі оболонки яких перетинаються.
Опуклі оболонки I і J повинні перетинатись, бо вони містять спільну точку
де
Лівий бік формули для p виражає цю точку як опуклу комбінацію точок з I, а правий бік виражає як опуклу комбінацію точок з J. Отже, p приналежить обом опуклим оболонкам, завершуючи доведення.
Це доведення дозволяє ефективну побудову точки Радона, за час поліноміальний від вимірності, із використанням методу Гаусса або іншого ефективного алгоритму для розв'язання системи лінійних рівнянь для множників.[1]
Примітки
Посилання
- Clarkson, Kenneth L.; Eppstein, David; Miller, Gary L.; Sturtivant, Carl; Teng, Shang-Hua (1996). Approximating center points with iterated Radon points. Int. J. Computational Geometry & Applications 6 (3): 357–377. MR 1409651. doi:10.1142/s021819599600023x..