Опукла множина
Опуклою множиною в евклідовому або афінному просторі називається така множина, яка разом з довільними двома точками, що належать множині, має у собі відрізок, що їх з'єднує[1].
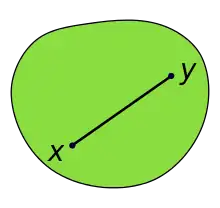
Опукла множина виглядає як деформоване коло. Чорний відрізок з'єднує точки x та y і розташований повністю в (зеленій) множині. Оскільки це виконується для будь-яких точок x та y множини, то множина буде опуклою.
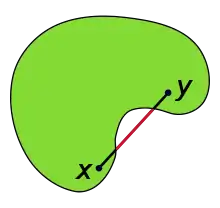
Приклад неопуклої множини. Так як червона частина (чорне та червоне) відрізку, що з'єднує точки x та y, розташована за межами (зеленої) множини, то множина не буде опуклою.
Визначення
- Іншими словами, множина називається опуклою, якщо для точок , що задаються радіус-векторами , точка:
- Тобто, множина разом з будь-якими двома точками , які належать цій множині, містить відрізок, який їх з'єднує:
- .
Приклади
У просторі опуклими множинами будуть точка, відрізок, інтервал, промінь, пряма.
У просторі опуклим буде сам простір, будь-який його лінійний підпростір, куля, опуклі множини просторів меншої вимірності. Також, опуклими будуть такі множини:
- пряма , що проходить через точку в напрямку вектора :
- ;
- промінь , який виходить із точки в напрямку вектора :
- ;
- гіперплощина Hpβ з нормаллю p:
- ;
- півпростори на які гіперплощина поділяє простір:
- ,
- .
Всі перелічені множини (крім кулі) є частковими випадками опуклої множини поліедру.
Чотирикутник на площині може бути опуклим і неопуклим.
Властивості опуклих множин
- Перетин опуклих множин є опуклим.
- Лінійна комбінація точок опуклої множини опукла.
- Опукла множина містить будь-яку опуклу комбінацію своїх точок.
- Будь-яку точку n-вимірного евклідового простору з опуклої оболонки множини можна представити як опуклу комбінацію не більш ніж n+1 точок цієї множини.
Див. також
Посилання
- Аналітична геометрія: Навч. посібник для студ. мат. спец. ун-тів: пер. с рус. / О. А. Борисенко, Л. М. Ушакова ; Пер. Г. Ч. Курінний. — Харків: Основа, 1993 . — 192 с.
Література
- Половинкин Е. С., Балашов М. В. Элементы выпуклого и сильно выпуклого анализа. — М. : ФИЗМАТЛИТ. — 416 с. — ISBN 5-9221-0499-3..
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.