Теорема галереї мистецтв

Теорема галереї мистецтв або музейна проблема — добре вивчена проблема видності в обчислювальній геометрії. Вона походить від реальної задачі охорони художньої галереї за допомогою найменшої можливої кількості камер, що можуть одночасно спостерігати за всією галереєю. В обчислювальній геометрії планування галереї описується за допомогою простого многокутника і кожна камера представлена точкою у многокутнику. Кажуть, що множина точок $S$ охороняє многокутник, якщо для кожної точки $p$ у многокутнику існує деяка точка $q\in S$ така, що відрізок між $p$ і $q$ не залишає цей многокутник.

Два виміри

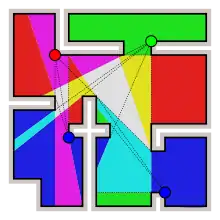
Чотири камера покривають цю галерею.

Наявні багато видозмін первісної проблеми, які також згадуються як задачі галереї мистецтв. У деяких версіях камери можна ставити лише уздовж периметра або навіть тільки у вершинах многокутника. Деякі версії вимагають спостереження лише за периметром, або його частиною.

Рішення задачі, в якій камери повинні бути розташовані на вершинах і охоронятися повинні тільки вершини, еквівалентне вирішенню задачі про домінівну множину на графі видимості багатокутника.

Теорема галереї мистецтв Шватала

Названа на честь Вацлава Шватала, задає верхню межу мінімальної кількості камер. Вона стверджує, що $\left\lfloor n/3\right\rfloor$ камер завжди достатньо, а іноді необхідно для охорони простого многокутника з $n$ вершинами.

Питання про те як багато вершин/хранителів/охоронців необхідно Шваталу поставив Віктор Клі у 1973.[1] Шватал довів теорема невдовзі по тому.[2] Доведення Шватала пізніше спростив Стів Фіск, використавши аргумент 3-розфарбування.[3]

Коротке доведення Фіска

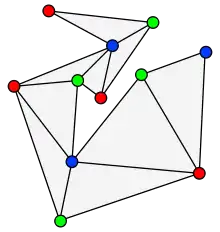
Розфарбування 3 кольорами вершин триангульованого многокутника. Сині вершини утворюють набір з трьох камер, настільки мало як і було гарантовано теоремою галереї мистецтв. Однак, цей набір не оптимальний: цей самий полігон можна охороняти за допомогою двох камер.

Fisk, (1978) довів теорему так.

По-перше, многокутник триангулюють (без додавання додаткових вершин. Тоді вершини многокутника 3-фарбують, так щоб кожний трикутник мав усі три кольори. Для знаходження 3-фарбування корисно звернути увагу на те, що двоїстий граф для триангуляції є деревом, будь-який цикл в двоїстому графі сформує границю дірки в многокутнику, що суперечить припущенню, що многокутник не мав дірок. Це означає, що ми можемо знайти 3-фарбування, використовуючи простий обхід графа як-от пошук у глибину.

Щойно 3-фарбування знайдено, вершини одного кольору утворюють підхожу множину для охорони, оскільки кожне трикутник охороняється його вершиною цього кольору. З того, що три кольори розбивають n вершин многокутника, колір з найменшою кількістю вершин формує правильну множину для охорони з не більше ніж $\lfloor n/3\rfloor$ камерами.

Обчислювальна складність

Версія задачі галереї мистецтв як проблема вибору звучить так: маємо многокутник і число k, а треба з'ясувати чи можливо охороняти цей многокутник за допомогою k камер. Ця задача і всі її стандартні варіації (такі як обмеження розташування камер самими вершинами або ребрами многокутника) є NP-складною.[4]

Однак, існують ефективні алгоритми для множини з не більше ніж $\lfloor n/3\rfloor$ камер, що відповідає верхній межі встановленій Шваталом. Таку множину можна знайти за час $O(n\log n).$ David Avis and Godfried Toussaint (1981) довів наявність такого алгоритму із використанням техніки розділяй та володарюй. Kooshesh та Moret, (1992) надав алгоритм лінійного часу, використовуючи доведення Фіска і алгоритм триангуляції лінійного часу Бернарда Чазела.

Узагальнення

Існує цілий ряд узагальнень і уточнень оригінальної теореми галереї мистецтв. Наприклад, для ортогональних багатокутників, чиї сторони перетинаються під прямим кутом, необхідно тільки $\lfloor n/4\rfloor$ камер. Є принаймні три докази цього результату, жоден з них не простий: Кана, Клейва і Клейтмана; Любіва; Сака і Туссена.

Схожі задачі намагаються визначити, скільки необхідно камер, щоб охопити екстер'єр галереї: $\lceil n/2\rceil$ — інколи необхідна і завжди достатня кількість. Іншими словами, нескінченний екстер'єр складніше охороняти, ніж скінченну галерею.

Три виміри

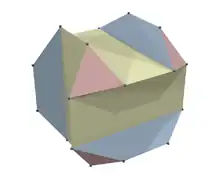
Приклад багатогранника з з внутрішніми точками не видними з жодної вершини.

Якщо музей представлено у трьох вимірах як багатогранник, тоді розташування камер у кожній вершині не гарантуватиме, що весь музей під спостереженням. Хоча всі многокутники, що утворюють поверхню спостерігатимуться, все ж залишаться точки, недоступні для камер.[5]

Примітки

O'Rourke, (1987), p. 1.
Chvátal, (1975).
Fisk, (1978).
O'Rourke, (1987), pp. 239—242; Aggarwal, (1984); Lee та Lin, (1986).
O'Rourke, (1987), p. 255.

Джерела

Aggarwal, A. (1984). The art gallery theorem: Its variations, applications, and algorithmic aspects. Ph.D. thesis, Johns Hopkins University..
Avis, D.; Toussaint, G. T. (1981). An efficient algorithm for decomposing a polygon into star-shaped polygons. Pattern Recognition 13 (6): 395–398. doi:10.1016/0031-3203(81)90002-9..
Brönnimann, H.; Goodrich, M. T. (1995). Almost optimal set covers in finite VC-dimension. Discrete and Computational Geometry 14 (1): 463–479. doi:10.1007/BF02570718..
Chvátal, V. (1975). A combinatorial theorem in plane geometry. Journal of Combinatorial Theory, Series B 18: 39–41. doi:10.1016/0095-8956(75)90061-1..
Couto, M.; de Rezende, P.; de Souza, C. (2011). An exact algorithm for minimizing vertex guards on art galleries. International Transactions in Operational Research: no–no. doi:10.1111/j.1475-3995.2011.00804.x..
Couto, M.; de Rezende, P.; de Souza, C. (2011). Benchmark instances for the art gallery problem with vertex guards..
Deshpande, Ajay; Kim, Taejung; Demaine, Erik D.; Sarma, Sanjay E. (2007). A Pseudopolynomial Time O(logn)-Approximation Algorithm for Art Gallery Problems. Proc. Worksh. Algorithms and Data Structures. Lecture Notes in Computer Science 4619. Springer-Verlag. с. 163–174. ISBN 978-3-540-73948-7. doi:10.1007/978-3-540-73951-7_15..
Eidenbenz, S.; Stamm, C.; Widmayer, P. (2001). Inapproximability results for guarding polygons and terrains. Algorithmica 31 (1): 79–113. doi:10.1007/s00453-001-0040-8. Архів оригіналу за 24 червня 2003. Процитовано 14 липня 2015..
Fisk, S. (1978). A short proof of Chvátal's watchman theorem. Journal of Combinatorial Theory, Series B 24 (3): 374. doi:10.1016/0095-8956(78)90059-X..
Ghosh, S. K. (1987). Approximation algorithms for art gallery problems. Proc. Canadian Information Processing Society Congress. с. 429–434..
Kahn, J.; Klawe, M.; Kleitman, D. (1983). Traditional galleries require fewer watchmen. SIAM J. Alg. Disc. Meth. 4 (2): 194–206. doi:10.1137/0604020..
Kooshesh, A. A.; Moret, B. M. E. (1992). Three-coloring the vertices of a triangulated simple polygon. Pattern Recognition 25 (4): 443. doi:10.1016/0031-3203(92)90093-X..
Lee, D. T.; Lin, A. K. (1986). Computational complexity of art gallery problems. IEEE Transactions on Information Theory 32 (2): 276–282. doi:10.1109/TIT.1986.1057165..
Lubiw, A. (1985). Decomposing polygonal regions into convex quadrilaterals. Proc. 1st ACM Symposium on Computational Geometry. с. 97–106. ISBN 0-89791-163-6. doi:10.1145/323233.323247..
O'Rourke, Joseph (1987). Art Gallery Theorems and Algorithms. Oxford University Press. ISBN 0-19-503965-3..
Sack, J. R.; Toussaint, G. T. (1988). Guard placement in rectilinear polygons. У Toussaint, G. T. Computational Morphology. North-Holland. с. 153–176..
Shermer, Thomas (1992). Recent Results in Art Galleries. Proceedings of the IEEE 80 (9): 1384–1399. doi:10.1109/5.163407..
Valtr, P. (1998). Guarding galleries where no point sees a small area. Israel J. Math. 104 (1): 1–16. doi:10.1007/BF02897056..

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] O'Rourke, (1987), p. 1.

[2] Chvátal, (1975).

[3] Fisk, (1978).

[4] O'Rourke, (1987), pp. 239—242; Aggarwal, (1984); Lee та Lin, (1986).

[5] O'Rourke, (1987), p. 255.