Теорема про бісектрису

Ілюстрація доведення теореми про бісектрису (методом пропорційних відрізків)

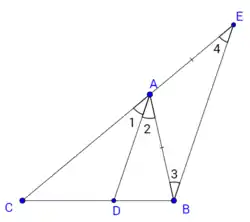
Нехай дано трикутник ${\displaystyle ABC}$, ${\displaystyle AD}$ — бісектриса кута ${\displaystyle \angle A}$. Через точку ${\displaystyle B}$ проведемо пряму, паралельну прямій ${\displaystyle AD}$ і нехай проведена пряма перетинає пряму ${\displaystyle AC}$ в точці ${\displaystyle E}$.

На зображенні кути ${\displaystyle 2}$ та ${\displaystyle 3}$ рівні як внутрішні різносторонні при паралельних прямих ${\displaystyle AD}$ і ${\displaystyle BE}$ та січній ${\displaystyle AB}$; кути ${\displaystyle 1}$ та ${\displaystyle 4}$ рівні як відповідні при паралельних прямих ${\displaystyle AD}$ і ${\displaystyle BE}$ та січній ${\displaystyle AE}$. Проте кути ${\displaystyle 1}$ та ${\displaystyle 2}$ рівні, оскільки ${\displaystyle AD}$ — бісектриса кута ${\displaystyle \angle A}$. Звідси маємо, що всі кути ${\displaystyle 1}$, ${\displaystyle 2}$, ${\displaystyle 3}$ та ${\displaystyle 4}$ рівні між собою. Звідси маємо, що трикутник ${\displaystyle ABE}$ рівнобедрений, тобто ${\displaystyle AE=AB}$.

За теоремою про пропорційні відрізки маємо: ${\displaystyle {\frac {CD}{AC}}={\frac {DB}{AE}}}$. Але ${\displaystyle AE=AB}$, тому ${\displaystyle {\frac {CD}{AC}}={\frac {DB}{AB}}}$, звідки остаточно${\displaystyle {\frac {BD}{DC}}={\frac {AB}{AC}}}$. Теорему доведено.

Ілюстрація доведення теореми про бісектрису (методом площ)

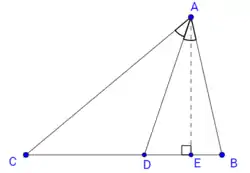
Нехай дано трикутник ${\displaystyle ABC}$, ${\displaystyle AD}$ — бісектриса кута ${\displaystyle \angle A}$. Знайдемо площі трикутників ${\displaystyle ABD}$ та ${\displaystyle ADC}$. Для цього скористаємося двома формулами для знаходження площ:

${\displaystyle S={\frac {1}{2}}ah_{a}}$, де ${\displaystyle a}$ — сторона трикутника, а ${\displaystyle h_{a}}$ — висота, опущена на цю сторону;

${\displaystyle S={\frac {1}{2}}bc\sin \alpha }$, де ${\displaystyle b}$ та ${\displaystyle c}$ — сторони трикутника, ${\displaystyle \alpha }$ — кут між цими сторонами.

З першої формули маємо, що ${\displaystyle S_{ABD}={\frac {1}{2}}BD\cdot AE}$, а ${\displaystyle S_{ADC}={\frac {1}{2}}CD\cdot AE}$, де ${\displaystyle AE}$ — висота трикутника ${\displaystyle ABC}$, яка є також і висотою трикутників ${\displaystyle ABD}$ та ${\displaystyle ADC}$. Звідси ${\displaystyle {\frac {S_{ABD}}{S_{ADC}}}={\frac {{\frac {1}{2}}BD\cdot AE}{{\frac {1}{2}}CD\cdot AE}}={\frac {BD}{DC}}}$.

З другої формули отримуємо, що ${\displaystyle S_{ABD}={\frac {1}{2}}AB\cdot AD\sin \angle BAD}$ та ${\displaystyle S_{ADC}={\frac {1}{2}}AC\cdot AD\sin \angle DAC}$. Звідси ${\displaystyle {\frac {S_{ABD}}{S_{ADC}}}={\frac {{\frac {1}{2}}AB\cdot AD\sin \angle BAD}{{\frac {1}{2}}AC\cdot AD\sin \angle DAC}}={\frac {AB\sin \angle BAD}{AC\sin \angle DAC}}}$. Оскільки ${\displaystyle AD}$ — бісектриса кута ${\displaystyle \angle A}$, то ${\displaystyle \angle BAD=\angle DAC}$, звідки ${\displaystyle \sin \angle BAD=\sin \angle DAC}$, а тому остаточно ${\displaystyle {\frac {S_{ABD}}{S_{ADC}}}={\frac {AB}{AC}}}$.

Вище доведено, що ${\displaystyle {\frac {S_{ABD}}{S_{ADC}}}={\frac {BD}{DC}}}$ та ${\displaystyle {\frac {S_{ABD}}{S_{ADC}}}={\frac {AB}{AC}}}$, а тому ${\displaystyle {\frac {BD}{DC}}={\frac {AB}{AC}}}$. Теорему доведено.

Якщо пряма ${\displaystyle AD}$ не обов'язково є бісектрисою, то з вище викладених міркувань випливає, що ${\displaystyle {\frac {BD}{DC}}={\frac {AB\sin \angle BAD}{AC\sin \angle DAC}}}$.

• Мерзляк А. Г., Полонський В. Б., Якір М. С. Геометрія: підруч. для 8 кл. з поглибл. вивченням математики. — Х.: Гімназія, 2009. — 240 с.  ISBN 978-966-474-012-5