Теорема Фалеса про пропорційні відрізки

Теорема Фалеса належить давньогрецькому математику і філософу Фалесу Мілетському. За легендою, Фалес Мілетський знаходив висоту піраміди Хеопса, вимірюючи довжину її тіні на землі та довжину тіні палиці, вимірюваної висоти. Найперше письмове доведення цієї теореми подано в книзі "Начала" (книга VI).боти. го у фф

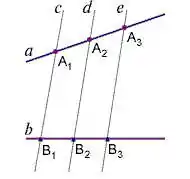
Теорема Фалеса: якщо паралельні прямі, що перетинають дві задані прямі а і b, відтинають на одній прямій рівні відрізки, то вони відтинають рівні відрізки й на іншій прямій.

${\displaystyle A_{1}A_{2}=A_{2}A_{3},}$ то ${\displaystyle B_{1}B_{2}=B_{2}B_{3}.}$

Узагальнена теорема Фалеса: паралельні прямі, що перетинають дві задані прямі а і b, відтинають на них пропорційні відрізки.

${\displaystyle {\frac {A_{1}A_{2}}{B_{1}B_{2}}}={\frac {A_{2}A_{3}}{B_{2}B_{3}}}={\frac {A_{1}A_{3}}{B_{1}B_{3}}}.}$

Малюнок 1

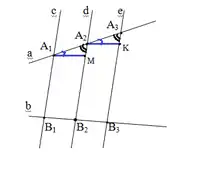
Нехай дано паралельні прямі ${\displaystyle A_{1}B_{1}\parallel }$ ${\displaystyle A_{2}B_{2}\parallel }$ ${\displaystyle A_{3}B_{3}}$ , які перетинають прямі ${\displaystyle a}$ і ${\displaystyle b}$, причому ${\displaystyle A_{1}A_{2}=A_{2}A_{3}}$ (дивитись праворуч Малюнок 1).

Через точки ${\displaystyle A_{1}}$ і ${\displaystyle A_{2}}$ проведено прямі ${\displaystyle A_{1}M}$ і ${\displaystyle A_{2}K}$, паралельні прямій ${\displaystyle b}$.

${\displaystyle \vartriangle A_{1}A_{2}M=\vartriangle A_{2}A_{3}K}$ за другою ознакою рівності трикутників, оскільки:

1)${\displaystyle A_{1}A_{2}=A_{2}A_{3}}$ - за умовою,

2)${\displaystyle \angle A_{1}A_{2}M=\angle A_{2}A_{3}K}$ - відповідні кути при паралельних прямих ${\displaystyle MA_{2}}$ і ${\displaystyle KA_{3}}$,

3)${\displaystyle \angle A_{1}MA_{2}=\angle A_{2}KA_{3}}$ - відповідні кути при паралельних прямих ${\displaystyle A_{1}M}$ і ${\displaystyle A_{2}K}$.

З рівності трикутників ${\displaystyle \vartriangle A_{1}A_{2}M=\vartriangle A_{2}A_{3}K}$ ${\displaystyle \Rightarrow }$${\displaystyle A_{1}M}$=${\displaystyle A_{2}K}$, як відповідні сторони рівних трикутників.

Малюнок 2

З побудови (Малюнок 1) чотирикутник ${\displaystyle A_{1}B_{1}B_{2}M}$ - паралелограм, тому ${\displaystyle A_{1}M=B_{1}B_{2}}$.

З побудови (Малюнок 1) чотирикутник ${\displaystyle A_{2}B_{2}B_{3}K}$ - паралелограм, тому ${\displaystyle A_{2}K=B_{2}B_{3}}$.

Звідси ${\displaystyle A_{1}M=A_{2}K}$ і ${\displaystyle B_{1}B_{2}=B_{2}B_{3}}$.

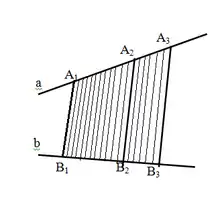
Нехай прямі ${\displaystyle a}$ і ${\displaystyle b}$ перетинають паралельні прямі у точках ${\displaystyle A_{1},A_{2},A_{3}}$ і ${\displaystyle B_{1},B_{2},B_{3}}$ відповідно (дивитись праворуч Малюнок 2).

Доведемо, що ${\displaystyle {\frac {A_{1}A_{2}}{A_{1}A_{3}}}={\frac {B_{1}B_{2}}{B_{1}B_{3}}}}$ для випадку, коли існує відрізок такої довжини ${\displaystyle \delta }$, який можна відкласти ціле число разів на відрізку ${\displaystyle A_{1}A_{3}}$ і ${\displaystyle A_{1}A_{2}}$. Нехай ${\displaystyle A_{1}A_{3}=n\delta }$, ${\displaystyle A_{1}A_{2}=m\delta }$ і ${\displaystyle n>m}$. Поділимо відрізок ${\displaystyle A_{1}A_{3}}$ на ${\displaystyle n}$ рівних частин (довжиною ${\displaystyle \delta }$), точка ${\displaystyle A_{2}}$- одна з точок поділу. Через точки поділу проведемо прямі, паралельні ${\displaystyle A_{3}B_{3}}$. За теоремою Фалеса ці прямі ділять відрізок ${\displaystyle B_{1}B_{3}}$ на рівні відрізки деякої довжини ${\displaystyle \delta _{1}}$. Отримаємо:${\displaystyle B_{1}B_{3}=n\delta _{1}}$, ${\displaystyle B_{1}B_{2}=m\delta _{1}}$, ${\displaystyle {\frac {A_{1}A_{2}}{A_{1}A_{3}}}={\frac {m\delta }{n\delta }}={\frac {m}{n}}}$ і ${\displaystyle {\frac {B_{1}B_{2}}{B_{1}B_{3}}}={\frac {m\delta _{1}}{n\delta _{1}}}={\frac {m}{n}}}$ ${\displaystyle \Longrightarrow }$ ${\displaystyle {\frac {A_{1}A_{2}}{A_{1}A_{3}}}={\frac {B_{1}B_{2}}{B_{1}B_{3}}}}$.

• Погорєлов О. В. Геометрія: Планіметрія: Підруч. для 7—9 кл. загальноосвіт. навч. закл. — 7-ме вид. — К. : Школяр, 2004. — С. 85—87.

• Фалеса теорема // Універсальний словник-енциклопедія. — 4-те вид. — К. : Тека, 2006.