Теорема про два вуха
В геометрії теорема про два вуха стверджує, що кожен простий багатокутник більш ніж з трьома вершинами має щонайменше два вуха, вершини, які можна вилучити з багатокутника без використання перетинів. Теорема про два вуха еквівалентна існуванню тріангуляції багатокутника. Її часто приписують Гері Х. Мейстерсу, але вона була доведена раніше Максом Деном.
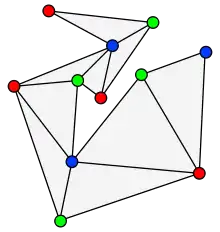
Твердження теореми
Вухо багатокутника визначається як вершина v така, що відрізок лінії між двома вершинами, які суміжні (з'єднані ребром) v, повністю лежить у внутрішній частині багатокутника. Теорема про два вуха стверджує, що кожен простий багатокутник має щонайменше два вуха.
Вуха та тріангуляція
Вухо та дві його суміжні вершини утворюють трикутник у межах багатокутника, який не перетинається жодною іншою частиною багатокутника. Якщо вилучити трикутник такого типу, утворюється багатокутник з меншою кількістю сторін, а багаторазове видалення вух дозволяє тріангулювати будь-який простий багатокутник.
І навпаки, якщо багатокутник трикутний, слабко двоїстий граф тріангуляції (граф в якому одна вершина відповідає одному трикутнику, а одне ребро — парі суміжних трикутників) буде деревом і кожен лист дерева відповідатиме вуху. Оскільки кожне дерево більш ніж з однією вершиною має щонайменше два листки, кожен тріангульований багатокутник, в якому більш ніж один трикутник, має принаймні два вуха. Таким чином, теорема про два вуха рівносильна тому, що кожен простий багатокутник має тріангуляцію[1].
Суміжні типи вершин
Вухо називають оголеним, коли воно утворює вершину опуклої оболонки багатокутника. Однак багатокутник може й не мати оголених вух[2].
Вуха є окремим випадком головної вершини, а саме такою, що відрізок лінії, який з'єднує суміжні вершини, не перетинає багатокутник і не торкається будь-якої іншої його вершини. Основна вершина, для якої цей відрізок не належить багатокутнику, називається ротом. Аналогічно теоремі про два вуха, кожен не опуклий простий багатокутник має щонайменше один рота. Багатокутники з мінімальною кількістю головних вершин обох типів, а саме, рівно з двома вухами та одним ротом, називаються антропоморфними багатокутниками[3].
Історія та докази
Теорему про два вуха часто пов'язують зі статтею Гарі Х. Мейстерса 1975 року, з якого і походить термінологія «вуха»[4]. Однак теорема була доведена раніше Максом Деном (близько 1899 року) як частина доказу теореми Жордана. Для доведення теореми, Ден зауважує, що кожен багатокутник має щонайменше три опуклі вершини. Якщо одна з цих вершин, v, не є вухом, то вона може бути з'єднана по діагоналі з іншою вершиною x всередині трикутника uvw утвореної v і двома його суміжними; x може бути вершиною у цьому трикутнику, та буде найвіддаленішою від лінії uw. Ця діагональ ділить багатокутник на два менші багатокутники, і повторний поділ на вуха та діагоналі призводить до тріангуляції всього многокутника, з якого вухо може бути знайдено як лист двоїстого дерева[5].
Примітки
- O'Rourke, Joseph (1987). Art Gallery Theorems and Algorithms. International Series of Monographs on Computer Science. Oxford University Press. ISBN 0-19-503965-3. MR 921437.
- Meisters, G. H. (1980). Principal vertices, exposed points, and ears. American Mathematical Monthly 87 (4): 284–285. MR 567710. doi:10.2307/2321563..
- Toussaint, Godfried (1991). Anthropomorphic polygons. American Mathematical Monthly 98 (1): 31–35. MR 1083611. doi:10.2307/2324033..
- Meisters, G. H. (1975). Polygons have ears. American Mathematical Monthly 82: 648–651. MR 0367792. doi:10.2307/2319703..
- Guggenheimer, H. (1977). The Jordan curve theorem and an unpublished manuscript by Max Dehn. Archive for History of Exact Sciences 17 (2): 193–200. JSTOR 41133486. MR 0532231. doi:10.1007/BF02464980..
Джерела
- Meisters' Two Ears Theorem, Cut-the-Knot (англ.)
- The Two-Ears Theorem, Готфрід Тусайн (англ.)
- Weisstein, Eric W. Two-Ears Theorem(англ.) на сайті Wolfram MathWorld.