Вершина (геометрія)

В геометрії вершина — особливий вид точки, яка описує кут або перетин геометричних фігур.

Визначення

Як кута
Вершиною кута називається точка, з якої два відрізки або промені виходять разом.

Вершиною кута є точка, з якої два промені або відрізки починаються, в якій зустрічаються або перетинаються (перетин).[1]

Як багатогранника

Вершина — кутова точка багатокутника, багатогранника, або іншого багатовимірного політопа, утвореного перетином ребер або граней об'єкта.[1]

У багатокутника вершина називається «опуклою», якщо внутрішній кут багатокутника, тобто кут, утворений двома ребрами при вершині, з багатокутником всередині кута, менше, ніж π радіан (180°, два прямих кути); в іншому випадку вершина називається «увігнутою» або «рефлексом».[2] В цілому, вершина багатогранника або політопу опукла, якщо перетин багатогранника або політопу з досить малою сферою з центром у вершині опуклий, та увігнута в протилежному випадку.

Вершини багатогранника пов'язані з вершинами графів так, що 1-кістяк багатогранника є граф, вершини якого відповідають вершинам багатогранника,[3] і тому граф можна розглядати як одновимірний симпліціальний комплекс, вершини якого є вершинами графу. Однак у теорії графів вершини можуть мати менше два інцидентних ребра, що, як правило, не дозволено для геометричних вершин. Існує також зв'язок між геометричними вершинами і вершинами кривої, її точок екстремальної кривини: в якомусь сенсі вершини багатокутника є точками нескінченної кривини, і якщо багатокутник наближається до гладкої кривої, вершиною буде точка екстремальної кривини поблизу кожного багатокутника.[4] Однак гладка крива, наближена до багатокутника, буде також мати додаткові вершини в точках, де кривина мінімальна.

Як плоскої плитки

Вершиною плоскої плитки або мозаїки є точка, де три або більше плиток стикаються;[5] в цілому, але не завжди, плитки теселяції є багатокутниками та вершинами мозаїки є також вершини її плиток. В цілому, теселяції можна розглядати як свого роду топологічний клітинний комплекс, так само як грані багатогранника або політопа; вершинами інших видів комплексів, таких як симпліціальні комплекси, є його нуль-вимірні грані.

Головна вершина
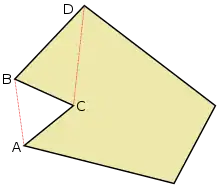
Вершина B — вухо, тому що інтервал між С і D повністю знаходиться всередині полігону. Вершина С — рот, тому що відкритий відрізок між А і В повністю знаходиться зовні багатокутника.

Вершина xi простого багатокутника Р є головною вершиною багатокутника, якщо діагональ [x(i−1),x(i+1)] перетинає границю Р тільки в точках x(i−1) та x(i+1). Існують два типи головних вершин: вухо і рот.[6]

Вухо

Кажуть, що головна вершина xi простого багатокутника P — вухо, якщо діагональ [x(i−1),x(i+1)], що відсікає xi, цілком лежить в P. (див. також опуклий многокутник) Теорема про два вуха стверджує, що кожен простий багатокутник має два вуха.[7]

Рот

Кажуть, що головна вершина xi простого багатокутника P — рот, якщо діагональ [x(i−1),x(i+1)] лежить зовні Р.

Кількість вершин багатогранника

Поверхня будь-якого опуклого багатогранника має ейлерову характеристику

де V — число вершин, E — число ребер, і F — число граней. Це рівняння відоме як формула Ейлера для багатогранника. Таким чином, число вершин на дві більше, ніж перевищення кількості ребер над числом граней. Наприклад, куб має 12 ребер, 6 граней і, отже, 8 вершин.

Вершини в комп'ютерній графіці

У комп'ютерній графіці об'єкти часто подаються як триангульовані багатогранники, в яких об'єкт вершини є пов'язаним не тільки з трьома просторовими координатами, але і з іншою графічною інформацією, необхідною для коректного відображення об'єкта, такою як кольори, властивості відображення, текстури і нормалі у вершинах;[8] ці властивості використовуються при поданні вершинних шейдерів та обробки вершин.

Посилання
  1. Heath, Thomas L. (1956). The Thirteen Books of Euclid's Elements (вид. 2nd ed. [Facsimile. Original publication: Cambridge University Press, 1925]). New York: Dover Publications.
    (3 vols.): ISBN 0-486-60088-2 (vol. 1), ISBN 0-486-60089-0 (vol. 2), ISBN 0-486-60090-4 (vol. 3). Heath's authoritative translation of Euclid's Elements plus his extensive historical research and detailed commentary throughout the text.
  2. Jing, Lanru; Stephansson, Ove (2007). Fundamentals of Discrete Element Methods for Rock Engineering: Theory and Applications. Elsevier Science.
  3. Peter McMullen, Egon Schulte, Abstract Regular Polytopes, Cambridge University Press, 2002. ISBN 0-521-81496-0 (Page 29)
  4. Alexander I. Bobenko, Peter Schröder, John M. Sullivan, Günter M. Ziegler (2008). Discrete differential geometry. Birkhäuser Verlag AG. ISBN 978-3-7643-8620-7.
  5. M.V. Jaric, ed, Introduction to the Mathematics of Quasicrystals (Aperiodicity and Order, Vol 2) ISBN 0-12-040602-0, Academic Press, 1989.
  6. Devadoss, Satyan; O'Rourke, Joseph (2011). Discrete and Computational Geometry. Princeton University Press. ISBN 978-0-691-14553-2.
  7. Meisters, G. H. (1975). Polygons have ears. The American Mathematical Monthly 82: 648–651. MR 0367792. doi:10.2307/2319703..
  8. Christen, Martin. Clockworkcoders Tutorials: Vertex Attributes. Khronos Group. Архів оригіналу за 12 квітня 2019.

Зовнішні зв'язки
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.