Теорема про метелика
Теорема про метелика — це класична теорема геометрії Евкліда, яку можна сформулювати так[1]:
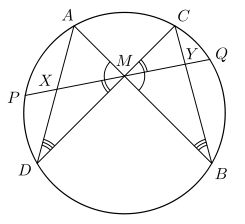
Нехай M — середина хорди PQ кола, через яку проведено дві інші хорди AB і CD; хорди AD і BC перетинають хорду PQ у точках X і Y відповідно. Тоді M — середина відрізка XY.
Доведення
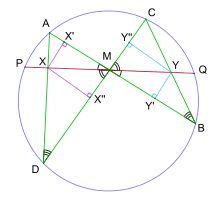
Формальне доведення теореми таке:
Нехай з точки X опущено перпендикуляри XX′ і XX″ на прямі AM і DM відповідно. Аналогічно, нехай з точки Y опущено перпендикуляри YY′ і YY″ на прямі BM і CM відповідно.
Оскільки має місце подібність трикутників
- за трьома кутами,
то
Аналогічно, будуть подібні трикутники
тому виконується
Також, будуть подібні трикутники
звідки
І, насамкінець, з подібності
тому
З попередніх рівнянь і теореми про відрізки хорд, що перетинаються, видно, що
оскільки PM = MQ.
Тому
Використавши основну властивість пропорції, маємо, що
Звівши подібні доданки
з обох сторін отриманого рівняння, отримаємо
Отже, MX = MY, оскільки довжини MX, MY та PM — це додатні дійсні числа.
Таким чином, M — середина XY .
Існують інші доведення[2], зокрема той, що використовує методи проективної геометрії[3].
Історія
Доведення теореми про метелика було представлено як розв'язок задачі Вільямом Воллесом у «The Gentlemen's Mathematical Companion» (1803). Три рішення були опубліковані в 1804 році, і в 1805 році сер Вільям Гершель знову поставив задачу в листі до Уоллеса. Преподобний Томас Скарр знову поставив те саме запитання в 1814 році в Gentlemen's Diary or Mathematical Repository[4].
Примітки
- Johnson, Roger A., Advanced Euclidean Geometry, Dover Publ., 2007 (orig. 1929).
- Martin Celli, «A Proof of the Butterfly Theorem Using the Similarity Factor of the Two Wings», Forum Geometricorum 16, 2016, 337—338. http://forumgeom.fau.edu/FG2016volume16/FG201641.pdf
- , problem 8.
- William Wallace's 1803 Statement of the Butterfly Theorem, cut-the-knot, retrieved 2015-05-07.
Посилання
- Теорема про метелика
- Краща теорема про метелика
- Доведення теореми про метелика на PlanetMath
- Теорема про метелика Джея Варендорфа
- Weisstein, Eric W. Теорема про метелика(англ.) на сайті Wolfram MathWorld.