Транзистор метал-діелектрик-напівпровідник

Звичайно вперше концепцію квазірівнів Фермі ввів Шоклі для опису металургійних p-n— переходів. Тому Са пішов тривіальним шляхом розповсюдження даної концепції на індуковані переходи. Індукований перехід відрізняється в першу чергу від металургійного тим, що на поверхні напівпровідника створюються тільки потенція для провідності оберненого типу відносно глибинних шарів напівпровідника. Тобто сам напівпровідник МДН-структури не має можливості для заповнення інверсними носіями поверхні напівпровідника, тому для цього по боках каналу формували кишені з інверсною провідністю відносно підкладки. Якщо цього не зробити, то отримаємо весь комплекс інерційних низькочастотних явищ в C- V- характеристиках МДН-структури (в районі 100 Герц). Другою особливістю індукованого переходу є те, що він є достатньо різкий відносно металургійного. Це обумовлено технологією обробки поверхні кремнію, котра є значно вища і контрольованіша за реальні металургійні переходи. Звичайно, вона ще далека від параметра решітки, проте вже достатньо близька до нього (в металургійних переходах такої різкості добитися взагалі не можливо). Справа в тому, що в «точці» самого переходу квазірівні електронів та дірок однакові за величиною і збігаються із серединою забороненої зони напівпровідника. Тобто в цій точці ми маємо власний напівпровідник, і тому чим тонша буде ця перехідна область (буде різкішою), тим ближче буде реальний перехід до ідеального, для якого розроблена мікроскопічна теорія.

Електрод затвора є основним керувальним електродом, котрий задає поверхневий потенціал напівпровідника МДН-структури, котра в свою чергу описується стандартним рівнянням Пуассона в ефекті поля. Тому при відсутності напруг на електродах стоку та підкладки (нульові значення) ми і отримуємо зв'язок між мікроскопічними потенціалами на поверхні розділу діелектрик- напівпровідник (${\displaystyle \phi _{s}}$) та макроскопічними напругами на затворі (${\displaystyle V_{G}}$) через теорему Гауса для зарядів на ємності МДН-структури. Звичайно цей стан поверхні напівпровідника з інверсною провідністю також є станом поперечної термодинамічної нерівноваги (тому поверхневий потенціал тут є також квазіпотенціалом Фермі), проте відсутність поперечного струму через МДН-структуру (наявність діелектрика!) дозволяє нехтувати тут нерівноважністю і вважати сам індукований перехід, як варіант металургійного. Очевидно, що це справедливо тільки для постійних напруг на затворі МДН-структури, а коли вона змінюється (при чому з великою частотою) то термодинамічна нерівноважність повинна вносити свої корективи в «ідеальний індукований перехід». Це приведе до того, що статичні параметри індукованого переходу будуть відрізнятися від динамічних.

Слід відзначити, що електрод підкладки виконує роль другого затвора, оскільки металізація підкладки знаходиться на нижній стороні МДН-структури. Проте він є неповноцінним в тому плані, що металізація підкладки не повністю покриває всю поверхню напівпровідника підкладки і може бути розташованим в будь- якому місці поверхні підкладки. В загальному випадку при подачі оберненої напруги ${\displaystyle V_{b}}$ на електрод підкладки буде збільшуватися товщина збідненої області, заряд якої задається виразом:

${\displaystyle Q_{d}\approx \pm {\sqrt {-2Nq\epsilon _{s}(V_{b}+2\phi _{F})}}}$,

де ${\displaystyle N}$ концентрація домішок (залежить від поверхневого потенціалу в загальному випадку), ${\displaystyle q}$- заряд електрона, ${\displaystyle \epsilon _{s}}$ діелектрична проникність напівпровідника та ${\displaystyle \phi _{F}}$- потенціал Фермі. Очевидно, що збільшення просторового заряду тривіально означає зменшення інверсного заряду (еквівалентне збільшенню «порогової напруги» МДН-структури). У випадку подачі прямої напруги на електрод підкладки, через джерельний перехід буде протікати прямий струм, як у звичайних металургійних переходах. Більше того, через електрод стоку також буде протікати додатковий струм, обумовлений прямою напругою на підкладці (т.з. «біполярний ефект»). Звичайно цей режим прямих напруг на підкладці на практиці не використовується (особливо в цифрових схемах), оскільки це є «паразитні» струми через стік.

Таким чином, вплив електрода підкладки на квазірівні Фермі не виходить за рамки концепції квазірівнів Фермі, розробленої для металургійних переходів.

До електроду стоку завжди прикладається обернена напруга, що викликає збільшення заряду збідненої області біля електроду стоку (ефект типовий для металургійних переходів). Тому до певної міри електрод стоку також виконує роль керувального електроду, подібно до електродів затвора та підкладки. Проте його вплив поступово зменшується з наближенням до електроду джерела вздовж каналу. Таким чином, електрод стоку виконує основну роль електроду прискорення неосновних носіїв, що з'являються біля електроду джерела, завдяки чому і створюється струм вздовж каналу. Звичайно не нульове значення напруги на електроді стоку створює поздовжнє електричне поле вздовж каналу, що своєю чергою створює умови для виникнення поздовжньої термодинамічної нерівноваги на поверхні розділу діелектрик- напівпровідник. Основна заслуга Са полягає в тому, що він припустив, що у випадку протікання стаціонарного струму вздовж каналу, електричне поле, а значить і поверхневий квазіпотенціал, обумовлений оберненою напругою на стоці, рівномірно розподіляється вздовж каналу не руйнуючи його енергетичної структури. Тобто, хоч поверхневий поперечний потенціал і поступово зменшується (тобто індукований перехід поступово зникає), проте вся поверхня веде себе цілісно, подібно до звичайного діелектрика (адже тільки в діелектриках ми маємо однорідне електричне поле, а збіднена область завжди веде себе подібно до діелектрика!). Знову ж таки ми тут маємо традиційне обмеження. Тобто отримані аналітичні вирази для інверсних зарядів, потенціалів та струмів вірні тільки у випадку протікання стаціонарного струму стоку, а у випадку змінного струму електричні параметри будуть іншими, оскільки концепція квазірівнів Фермі по Са і тут уже не буде працювати.

Заряд інверсного шару ${\displaystyle Q_{n}}$ знаходиться із умови електронейтральності (закон Гауса):

${\displaystyle Q_{n}+Q_{d}+Q_{ss}+Q_{G}=0\ }$

де заряд металічного затвора

${\displaystyle Q_{G}=C_{0}(V_{G}-\phi _{s}-\phi _{MS})\ }$,

а ${\displaystyle C_{0}}$- ємність діелектрика і :${\displaystyle \phi _{MS}}$ контактна різниця потенціалів метал- напівпровідник. Тоді інверсний заряд можна подати у формі:

${\displaystyle Q_{n}\approx -Q_{ss}\pm {\sqrt {-2Nq\epsilon _{s}(V_{b}+2\phi _{F}}}-C_{0}(V_{G}-V_{S}-\phi _{s}(V_{S})-\phi _{MS}\ }$

де ${\displaystyle V_{S}}$ — макроскопічний потенціал вздовж каналу (збігається з мікроскопічним!), який біля електрода стоку збігається із стоковою напругою.

Таким чином, подача змінної напруги на електрод затвора в потенції може зруйнувати як поперечну, так і поздовжню термодинамічну квазірівновагу, а значить і концепція квазірівнів Фермі Шоклі-Са буде не придатна для опису вольт- амперних характеристик (ВАХ) МДН-транзистора. Тому використовують поняття малих сигналів (малого збурення в термінах рівноважної термодинаміки), при яких концепція квазірівнів Фермі ще виконується. Очевидно, що поняття «малості» відноситься до вихідного сигналу на електроді стоку (амплітуда вихідного змінного сигналу є значно менша за напругу на стоці).

Інверсний канал та вплив на нього напруги на стоці U_DS ≠ 0)

При отриманні аналітичних виразів для ВАХ МДН-транзисторів використовують такі припущення:

1) виродження в напівпровіднику відсутнє;

2) ефективна рухливість ${\displaystyle \mu _{n}^{*}}$ носіїв заряду в інверсному шарі та еквівалентний поверхневий заряд ${\displaystyle Q_{ss}}$ не залежить від електричного поля;

3) підкладка легована однорідно і має велику товщину (тобто товщина збідненої області менша за товщину підкладки при любих напругах на стоці);

4) дифузний струм в каналі достатньо малий порівняно з дрейфовим струмом, тому ним можна знехтувати;

5) генерацією та рекомбінацією в області каналу можна знехтувати;

6) обернені струми металургійних переходів стік- підкладка та джерело- підкладка достатньо малі і тому також не враховуються.

В загальному випадку дрейфовий струм стоку ${\displaystyle I_{D}}$ записується у вигляді:

${\displaystyle I_{D}=Z\int _{0}^{x_{d}}j(x,y)\,dx}$

де ${\displaystyle j-}$ густина струму, а ${\displaystyle x_{d}-}$ товщина інверсійного каналу. Оскільки густину струму можна представити у вигляді (чисто дрейфовий струм):

${\displaystyle j(x,y)=-q\mu _{n}n{\frac {dV(y)}{dy}},}$

а інверсний заряд апроксимується двовимірним (поверхневим) інверсним зарядом з ефективною рухливістю:

${\displaystyle \int _{0}^{x_{d}}q\mu _{n}n\,dx=\mu _{n}^{*}Q_{n}(y),}$

тому маємо:

${\displaystyle I_{D}=-\mu _{n}^{*}ZQ_{n}(y){\frac {dV(y)}{dy}}.}$

У цих співвідношеннях використані такі позначення: ${\displaystyle n}$ та ${\displaystyle \mu _{n}-}$ для концентрації електронів та їхньої рухливості, ${\displaystyle Q_{n}(y)-}$ заряд інверсного шару в розрахунку на одиницю площі, ${\displaystyle V(y)-}$ потенціал поверхні каналу відносно електрода джерела, ${\displaystyle Z-}$ ширина каналу. Як бачимо, в рамках даного підходу реальна товщина інверсного каналу не враховується, а залежність рухливості по глибині також ігнорується введенням її ефективного значення. Для визначення величини ${\displaystyle Q_{n}(y)-}$ використаємо вираз наведений в попередньому розділі із відповідною заміною змінних:

${\displaystyle V_{S}=V(y)-V_{BS}\ }$

${\displaystyle V_{G}=V_{GS}-V_{BS}\ }$

${\displaystyle \phi (V_{S})=\phi _{S0}\approx 2\phi _{F}\ }$,

де ${\displaystyle \phi _{S0}-}$ поверхневий потенціал при ${\displaystyle y=0;}$; ${\displaystyle V_{GS}-}$ різниця потенціалів між електродами затвора та джерела. Таким чином, інверсний заряд на одиницю площі буде:

${\displaystyle Q_{n}(y)={\sqrt {-2Nq\epsilon _{s}[V(y)-V_{BS}+2\phi _{F}]}}-C_{0}[V_{GS}-V(y)-2\phi _{F}-\phi _{MS}]-C_{0}V_{ss}}$

В цьому виразі перший член відповідає заряду збідненої області підкладки, другий- заряд затворів, а третій — еквівалентний поверхневий заряд:

${\displaystyle V_{ss}=Q_{ss}/C_{0}\ }$.

Інтегруючи вираз для струму стоку по ${\displaystyle y}$ від 0 до ${\displaystyle L}$, а також враховуючи що ${\displaystyle I_{D}=const(y)}$, знаходимо аналітичний вираз для струму стоку:

${\displaystyle I_{D}={\frac {C_{0}\mu _{n}^{*}Z}{L}}{\big \{}V_{DS}(V_{GS}-V_{X})-{\frac {V_{DS}^{2}}{2}}-{\frac {2}{3}}({\frac {2|N|q\epsilon _{s}}{C_{0}^{2}}})^{1/2}\cdot [(V_{DS}-V_{BS}+2\phi _{F})^{3/2}-(2\phi _{F}-V_{BS})^{3/2}]{\big \}}}$

де ${\displaystyle V_{X}=\phi _{MS}+2\phi _{F}-V_{ss},\ }$

а ${\displaystyle V_{DS}-}$ напруга стік- джерело.

Якщо концентрація нескомпенсованих домішок ${\displaystyle N}$ в підкладці мала, а ємність оксиду ${\displaystyle C_{0}-}$ велика, тоді третій член в останньому виразі може стати достатньо малим, щоби ним знехтувати, так що отримуємо т.з. формулу Са:

${\displaystyle I_{D}\approx {\frac {C_{0}\mu _{n}^{*}Z}{L}}[V_{DS}(V_{GS}-V_{X})-{\frac {V_{DS}^{2}}{2}}].}$

Звичайно цей простий вираз в деяких випадках є недостатньо точним, тому кращі результати при ${\displaystyle V_{DS}\to 0}$ можна отримати при розкладі третього члена в ряд:

${\displaystyle I_{D}\approx {\frac {C_{0}\mu _{n}^{*}ZV_{DS}}{L}}{\big \{}V_{GS}-V_{X}-{\sqrt {\frac {-2Nq\epsilon _{s}(2\phi _{F}-V_{BS}}{C_{0}^{2}}}}{\big \}}}$

Із останнього виразу ясно, що ${\displaystyle I_{D}}$ прямує до нуля при

${\displaystyle V_{GS}=V_{T}=V_{X}+{\sqrt {\frac {-2Nq\epsilon _{s}(2\phi _{F}-V_{BS}}{C_{0}^{2}}}}}$.

Величина ${\displaystyle V_{T}}$ називається порогова напруга МДН-транзистора. Не важко помітити, що закривання струму стоку при любих напругах ${\displaystyle V_{DS}}$ буде протікати при напругах на затворі, також такими, що визначаються останнім співвідношенням. Дійсно, при конечному ${\displaystyle V_{DS}}$ та ${\displaystyle I_{D}=0}$, ${\displaystyle V(y)=0}$ і при ${\displaystyle Q_{N}(y)=0}$.

Типові ВАХ МДН-транзистора

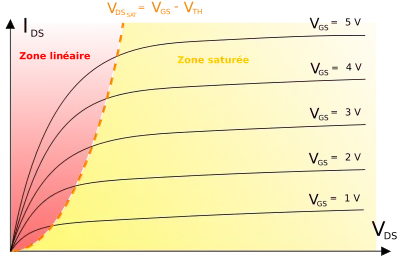
Напруга ${\displaystyle V_{DSat}=V_{GS}-V_{T}}$- називається напругою насичення/відсічки (тобто канал біля електроду стоку повністю перекривається для інверсних носіїв), коли струм стоку стає незалежним від напруги на стоці. В цьому разі, в області насичення ВАХ МДН-транзистора описуються простим виразом:

${\displaystyle I_{DSat}\approx {\frac {C_{0}\mu _{n}^{*}ZV_{DSat}^{2}}{2L}}=\beta {\frac {V_{DSat}^{2}}{2}}}$,

де ${\displaystyle \beta ={\frac {C_{0}\mu _{n}^{*}Z}{L}}-}$ питома крутизна ВАХ МДН-транзистора, широко вживана в практичних використаннях.

Режим слабої інверсії (weak inversion) вперше був досліджений в МДН-транзисторах Свенсоном та Мейндлом на початку 70-х років (тобто значно пізніше за режим сильної інверсії). На теренах Союзу цей режим був названий з легкої руки Д.Ігумнова — «мікрорежимом», оскільки в цьому разі під ним розумівся також режим експоненційних ВАХ в звичайних польових транзисторах з p-n— переходом. В межах підходу Свенсона- Мейндла зв'язок між мікроскопічними та макроскопічними потенціалами здійснювався за рахунок переходу:

${\displaystyle \phi _{s}-\phi _{c}-2\phi _{F}\approx {\frac {V_{G}-V_{T}(\phi _{c})}{m}}\ }$,

в якому використовувався ${\displaystyle m}$-фактор неідеальності індукованого p-n— переходу:

${\displaystyle m={\frac {C_{0}+C_{d}+C_{fs}}{C_{0}}},\ }$

де ${\displaystyle C_{d}-}$ питома ємність області просторового заряду (ОПЗ) на одиницю площі, ${\displaystyle C_{fs}-}$ питома ємність швидких поверхневих станів, а ${\displaystyle \phi _{c}=\phi _{Fn}-\phi _{Fp}}$ різниця квазірівнів Фермі. Спрощений вираз для струму стоку МДН-транзистора, який працює в режимі слабої інверсії на пологій ділянці стокових ВАХ за Свенсоном та Мейндлом:

${\displaystyle I_{dWI}\approx \beta (m\phi _{T})^{2}\cdot \exp({\frac {V_{G}-V_{T}}{m\phi _{T}}}),}$

де ${\displaystyle \phi _{T}=kT/q-}$ температурний потенціал, а ${\displaystyle k-}$ стала Больцмана.

Основним недоліком підходу Свенсона- Мейндла для мікрорежиму та Са для сильної інверсії а також інших, заснованих на подібних твердженнях, є неможливість знаходження товщини індукованого каналу (${\displaystyle x_{in}}$), а також неможливість коректного введення диференційного опору ${\displaystyle R_{i}}$ на пологій ділянці стокових ВАХ, який би базувався на загальних мікроскопічних принципах.

Проблема диференційного опору для режиму слабої інверсії МДН-транзистора з розподілом Максвелла- Больцмана для носіїв заряду була розв'язана в численних роботах Якимахи. В рамках даного підходу використовувалися такі припущення:

1) струм стоку визначається явищем дифузії;

2) індукований канал МДН-транзистора розбивається на дві області. В першій області (${\displaystyle 0\leq x\leq x_{gen}}$) градієнт концентрації носіїв заряду ${\displaystyle \nabla n}$ є функція, котра залежить від положення квазірівнів Фермі, а в другій області (${\displaystyle x_{gen}\leq x\leq x_{gen}+x_{dif}}$) — градієнт концентрації є постійний.

${\displaystyle I_{dWI}\approx (I_{0}+{\frac {V_{ds}}{R_{0}}})\exp({\frac {V_{gs}-V_{T}}{m\phi _{T}}})}$

${\displaystyle I_{0}\approx qD(-N_{A})L_{z}x_{gen}/L_{y},}$

${\displaystyle R_{0}\approx {\frac {m\phi _{T}L_{y}}{qL_{z}D(-N_{A})x_{dif}}},}$

де ${\displaystyle I_{0},R_{0}-}$ відповідно масштабні теплові: струм та диференційний опір МДН-транзистора, котрі розділяють режими слабої та сильної інверсії при ${\displaystyle V_{G}=V_{T}}$; ${\displaystyle D-}$ коефіцієнт дифузії. Основною особливістю даної напівфеноменологічної моделі є те, що тут присутні дві складові струму стоку: генеративна ${\displaystyle I_{0}}$, яка протікає крізь першу область (${\displaystyle 0\leq x\leq x_{gen}}$) індукованого каналу (ближче до поверхні розділу діелектрик- напівпровідник), та диференційна ${\displaystyle simV_{ds}/R_{0}}$, яка протікає крізь другу область індукованого каналу (${\displaystyle x_{gen}\leq x\leq x_{gen}+x_{dif}}$).

В межах даного підходу досить цікаво отримати основні підсилювальні параметри МДН-транзистора в режимі слабкої інверсії. Так, наприклад крутизна сток- затворної ВАХ тут буде:

${\displaystyle S_{g}={\frac {\partial I_{dWI}}{\partial V_{GS}}}={\frac {1}{m\phi _{T}}}(I_{0}+{\frac {V_{DS}}{R_{0}}})\exp({\frac {V_{gs}-V_{T}}{m\phi _{T}}})}$

а диференційний опір:

${\displaystyle R_{i}={\frac {1}{\frac {\partial I_{dWI}}{\partial V_{DS}}}}=R_{0}\exp({\frac {-V_{gs}+V_{T}}{m\phi _{T}}})}$

Знаючи крутизну та диференційний опір, знаходимо коефіцієнт підсилення МДН-транзистора в режимі слабкої інверсії:

${\displaystyle M_{gi}={\frac {I_{0}R_{0}+V_{DS}}{m\phi _{T}}}\approx {\frac {I_{0}R_{0}}{m\phi _{T}}}\ }$

у випадку, коли ${\displaystyle V_{DS}\ll I_{0}R_{0}\ }$. Тут треба відзначити, що коефіцієнт підсилення виявляється залежить від фундаментальних параметрів МДН-транзистора:

${\displaystyle M_{gi}\approx {\frac {I_{0}R_{0}}{m\phi _{T}}}={\frac {x_{gen}}{x_{dif}}}\ }$,

тобто є безрозмірним відношенням товщин інверсійного каналу.

Підхід Якимахи до слабкої інверсії також можна розповсюдити на режим сильної інверсії МДН-транзистора. Тут також можна розбити інверсійний канал на дві частини (генеративну та диференційну), при чому в обох цих частинах буде протікати дрейфовий струм стоку. Проте тільки в генеративній частині каналу буде справедливий підхід Са, а в диференціальній, інверсний заряд буде не залежний від поздовжнього електричного поля, обумовленого напругою на стоці. В області насичення можна ВАХ апроксимувати так:

${\displaystyle I_{dSI}\approx (I_{0SI}+2{\frac {V_{DS}}{R_{0SI}}}{\frac {m_{SI}\phi _{T}}{V_{GS}-V_{T}}})({\frac {V_{GS}-V_{T}}{m_{SI}\phi _{T}}})^{2}}$,

де

${\displaystyle I_{0SI}={\frac {\beta _{gen}(m_{SI}\phi _{T})^{2}}{2}}}$

та

${\displaystyle R_{0SI}={\frac {2}{\beta _{dif}m_{SI}\phi _{T}}}}$

масштабні параметри для струму стоку та диференційного опору в режиму сильної інверсії, а ${\displaystyle \beta _{gen}=\mu _{gen}{\frac {C_{0}Z}{L}}}$ та ${\displaystyle \beta _{dif}=\mu _{dif}{\frac {C_{0}Z}{L}}}$ — відповідно питомі крутизни для генеративної та диференціальної частин струму стоку.

Крутизна стокової характеристики тут буде:

${\displaystyle S_{g}={\frac {\partial I_{dSI}}{\partial V_{GS}}}={\frac {2I_{0SI}(V_{GS}-V_{T})}{(m_{SI}\phi _{T})^{2}}}+{\frac {2V_{DS}}{R_{0}m_{SI}\phi _{T}}}}$,

а диференційний опір

${\displaystyle R_{i}={\frac {1}{\frac {\partial I_{dSI}}{\partial V_{DS}}}}={\frac {R_{0SI}m_{SI}\phi _{T}}{2(V_{GS}-V_{T})}}}$.

Таким чином, можна записати коефіцієнт підсилення МДН-транзистора в режимі значної інверсії у вигляді:

${\displaystyle M_{gi}=S_{g}R_{i}={\frac {V_{DS}}{V_{GS}-V_{T}}}+{\frac {R_{0SI}I_{0SI}}{m_{SI}\phi _{T}}}\approx {\frac {R_{0SI}I_{0SI}}{m_{SI}\phi _{T}}}={\frac {\mu _{gen}}{\mu _{dif}}}}$.

Треба відзначити, що якби виконувалося співвідношення ${\displaystyle \beta _{gen}=\beta _{dif}}$, тоді коефіцієнт підсилення був би рівний одиниці ${\displaystyle M_{0SI}=1}$. Проте практика показує, що коефіцієнт підсилення МДН-транзистора навіть в режимі значної інверсії набагато більший від одиниці ${\displaystyle M_{SI}\gg 1}$. Тому насправді ми маємо відношення ${\displaystyle \beta _{gen}\gg \beta _{dif}}$, що автоматично означає неоднакові значення ефективної рухливості в генеративній та диференціальній частинах інверсного каналу ${\displaystyle \mu _{gen}\gg \mu _{dif}}$.