Трикутна хвиля
Трикутна хвиля — це несинусоїдальна форма хвилі, названа на честь своєї трикутної форми. Це періодична, кусково-лінійна, неперервна, дійснозначна функція.
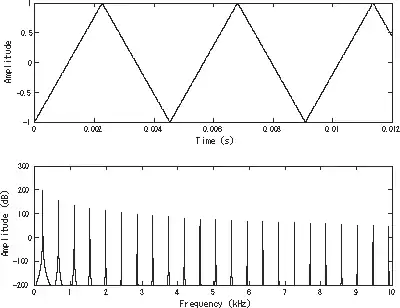
Як і прямокутна хвиля, трикутна хвиля містить тільки непарні гармоніки. Однак вищі гармоніки скочуються набагато швидше ніж в прямокутної хвилі (пропорційно оберненому квадрату номера гармоніки, а не оберненому значенню).
Гармоніки
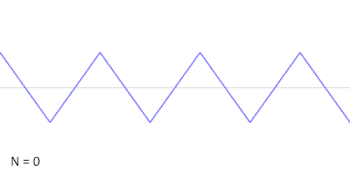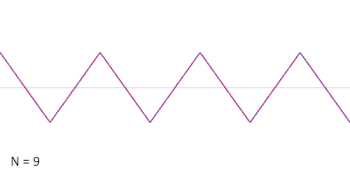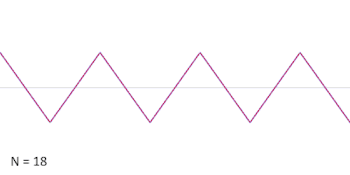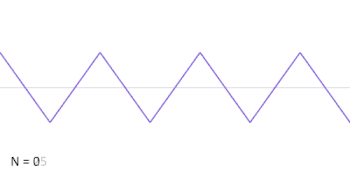
Можна апроксимувати трикутну хвилю адитивним синтезом, підсумовуючи непарні гармоніки основної частоти, домножуючи кожну іншу непарну гармоніку на (або, еквівалентно, змінюючи її фазу на π) і домножуючи амплітуду гармонік на обернений квадрат їх номера моди (або на обернений квадрат їх відносної частоти до фундаментальної).
Вищесказане можна математично узагальнити наступним чином:
- ,
де — кількість гармонік, що включаються в наближення, — незалежна змінна (наприклад, час для звукових хвиль), — основна частота, а — індекс гармоніки, яка пов'язана з номером її моди, .
Цей нескінченний ряд Фур'є сходиться до трикутної хвилі, коли прямує до нескінченності як показано на анімації.
Означення
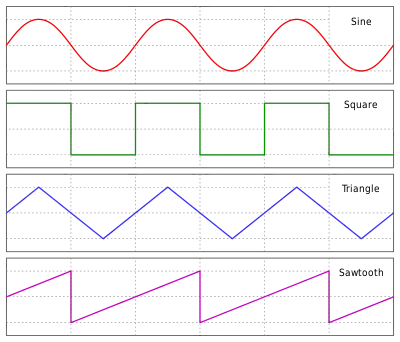
Ще одне означення трикутної хвилі на інтервалі від до та з періодом :
- ,
де символ — функція підлоги від .
Також трикутна хвиля може бути абсолютним значенням пилкоподібної хвилі :
або для інтервалу від до :
Трикутна хвиля також може бути виражена як інтеграл
- .
Це просте рівняння з періодом та початковим значенням :
- .
Оскільки у цьому представлені використовується лише функція модулята абсолютне значення, то це можна використовувати для простої реалізації трикутної хвилі на апаратній електроніці з малою потужністю процесора. Попереднє рівняння можна узагальнити на випадок періоду , амплітуди і початкового значення :
Попередня функція - це частковий випадок останньої при і :
Непарну версію першої функції можна отримати, просто змістити на одиницю початкове значення, що змінить фазу вихідної функції:
Узагальнюючи це, одержуємо непарну функцію для будь-якого періоду і амплітуди:
За допомогою функцій sine та arcsine з періодом та амплітудою трикутну хвилю можна записати у вигляді:
Довжина дуги
Довжина дуги за період для трикутної хвилі заданої амплітуди та періодом :
Дивись також
- Список періодичних функцій
- Кусково-лінійна функція
- Основна частота
- Зигзаг
- Синусоїда
- Прямокутна хвиля
- Функція підлоги та стелі
- Абсолютне значення
- Функція модуля
- Адитивний синтез
- Пилкоподібна хвиля
Посилання
- Weisstein, Eric W. Fourier Series - Triangle Wave(англ.) на сайті Wolfram MathWorld.