Тропічна геометрія
Тропічна геометрія — область в математиці, що з'явилася в 2000-ні, початково виникла в інформатиці, і пов'язана з алгебричною та симплектичною геометрією. Досліджувані в ній об'єкти є границею образів амеб звичайних алгебричних многовидів при виродженні останніх.[1]
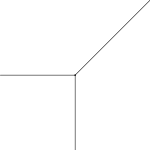
Тропічна пряма на площині
Назва «тропічна» віддає честь бразильській школі[1] — піонерським роботам бразильського математика Імре Сімона[2][3][4], який досліджував тропічне напівкільце у зв'язку з питаннями інформатики та теорії оптимізації[5].
Основні поняття
- Тропічне напівкільце (або тропічне напівполе) — множина дійсних чисел , оснащене операціями тропічного додавання і тропічного множення
- Тропічний многочлен ступеня на площині — кусково-афінна функція виду
Аналогічно, тропічний многочлен в загальному випадку — кусково-афінна функція виду
- Тропічна крива на площині, що відповідає даному тропічному многочлену ступеня — граф на площині, вершини і ребра (скінченні і нескінченні) якого утворюють множину точок негладкості функції . Ребра цього графу вважаються оснащеними кратностями: ребро, що розділяє області лінійності, які відповідають набору ступенів і , оснащується кратністю, рівною найбільшому спільному дільнику різниць і .
- Зокрема, тропічна пряма є об'єднанням трьох променів, що виходять з деякої точки і спрямовані вниз, вліво і вправо-вгору під 45 градусів. Тропічні прямі мають властивості, аналогічні властивостям звичайних прямих: через будь-які дві точки загального положення проходить рівно одна тропічна пряма, і дві тропічні прямі загального положення перетинаються в єдиній точці.
Примітки
- Itenberg, Mikhalkin, Shustin. Tropical algebraic geometry, 2009, с. vii.
- Архівована копія. Архів оригіналу за 26 вересня 2006. Процитовано 8 січня 2012.
- http://www.unn.ru/pages/issues/vestnik/9999-0217_West_matem_2003/18.pdf
- http://theor.jinr.ru/~belyov/articles/Litvinov_dequantize.pdf%5Bнедоступне+посилання+з+травня+2019%5D
- http://www.warwick.ac.uk/staff/D.Maclagan/papers/TropicalBook.pdf
Література
- Itenberg I., Mikhalkin G., Shustin E. Tropical algebraic geometry. — Basel : Springer, 2009. — viii+104 с. — (Oberwolfach Seminars)
- М. Э. Казарян, Тропическая геометрия, записки лекций.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.
