Тріангуляція поверхні

Тріангуляція поверхні може означати

  • мережу трикутників, яка покриває дану поверхню частково чи повністю або
  • процедуру побудови точок і трикутників цієї мережі
Тріангуляція неявної поверхні третього роду
Тріангуляція параметричної поверхні (мавпячого сідла)

У цій статті описується побудова мережі трикутників. Також в списку літературі можна знайти статті, які описують оптимізацію мережі.

Тріангуляція поверхні важлива для

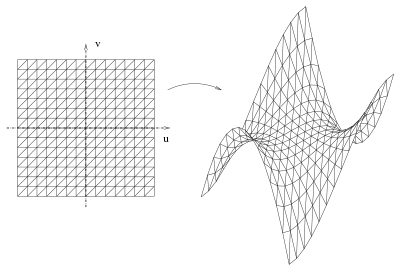
Тріангуляція параметрично заданої поверхні досягається шляхом тріангуляції області визначення цієї поверхні (див. малюнок на якому зображено мавпяче сідло). Однак трикутники можуть відрізнятися за формою і протяжністю в об'єктному просторі, що є потенційним недоліком. Це може бути зведено до мінімуму за допомогою адаптивних методів, які враховують ширину кроку при тріангуляції області параметрів.

Складніше тріангулювати неявну поверхню, яка визначена одним або декількома рівняннями. Існує два принципових підходи.

  • У першому методі тривимірну область, яка розглядається, розбивається на куби і визначається перетин поверхні з ребрами кубів, для того щоб отримати багатокутники на поверхні, які потім будуть тріангульовані. Такий підхід називається методом розрізання на куби (англ. cutting cube method)[1][2]. Він потребує суттєвих обчислювальних ресурсів.
  • Друга і простіша концепція — це маршовий метод (англ. marching method)[3][4][5]. Тріангуляція починається з тріангульованого шестикутника в початковій точці. Цей шестикутник потім оточується новими трикутниками, відповідно до заданих правил, поки вся поверхня не буде тріангульована. Якщо поверхня складається з декількох компонентів, то алгоритм потрібно запустити декілька разів з початковими точками на цих компонентах.

Алгоритм розрізання на куби визначає всі компоненти поверхні в межах початкового куба в залежності від заданих граничних параметрів. Перевагою маршового методу є можливість попереднього визначення границі (див. малюнок).

Полігонізація поверхні означає утворення полігональної сітки.

Тріангуляцію поверхні не слід плутати з тріангуляцією множини точок на площині. Прикладом якої є тріангуляція Делоне.

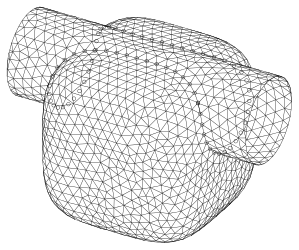  • Тріангуляція: циліндр та поверхня
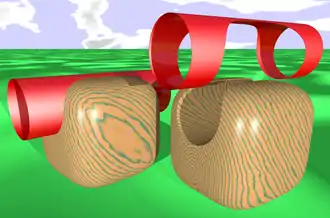  • Тріангуляція: циліндр та поверхня , зображення створене за допомогою POV-Ray
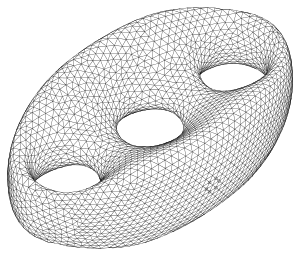
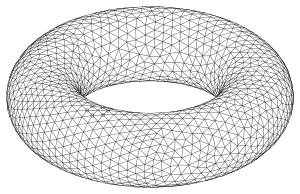  • Тор: тріангуляція маршовим методом
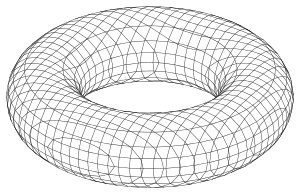  • Тор: тріангуляція методом розрізання на куби

Див. також

Список літератури
  1. M. Schmidt: Cutting Cubes — visualizing implicit surfaces by adaptive polygonization. Visual Computer (1993) 10, pp. 101—115
  2. J. Bloomenthal: Polygonization of implicit surfaces, Computer Aided Geometric Design (1988), pp. 341—355
  3. E. Hartmann: Geometry and Algorithms for COMPUTER AIDED DESIGN, p. 81
  4. E. Hartmann: A marching method for the triangulation of surfaces, The Visual Computer (1998), 14, pp. 95–108
  5. S. Akkouche & E Galin: Adaptive Implicit Surface Polygonization Using Marching Triangles, COMPUTER GRAPHICS forum (2001), Vol. 20, pp. 67–80

Посилання
  • Tasso Karkanis & A. James Stewart: Curvature-Dependent Triangulation of Implicit Surfaces
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.