Увігнутий многокутник

Увігнутий многокутник[1] або неопуклий многокутник[2] — це простий многокутник, який не є опуклим. Увігнутий многокутник буде завжди мати принаймні один тупий внутрішній кут — тобто кут, який знаходиться виключно між 180 і 360 градусами.[3]

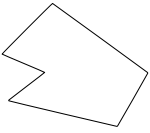
Приклад увігнутого багатокутника.

Властивості

Деякі прямі, що містять внутрішні точки увігнутого багатокутника, перетинають його межу більш ніж у двох точках.[3] Деякі діагоналі увігнутого багатокутника лежать частково або повністю поза ним.[3] Деякі бічні прямі, проведені через сторону увігнутого багатокутника не можуть розділити площину на дві півплощини так, щоб многокутник повністю належав одній з них. Жодне з цих трьох тверджень не виконується для опуклого багатокутника.

Як і для будь-якого простого багатокутника, сума внутрішніх кутів увігнутого багатокутника становить π (n   —   2) радіан, або 180 ° × (n   —   2), де n — кількість сторін.

Завжди можна розділити увігнутий многокутник на множину опуклих многокутників. Алгоритм, який виконує декомпозицію на якомога меншу кількість опуклих багатокутників за поліноміальний час описується Chazelle та Dobkin, (1985).[4]

Трикутник ніколи не може бути увігнутим, але існують увігнуті полігони з n сторін для будь-якого n > 3. Прикладом увігнутого чотирикутника є дельтоїд.

Принаймні один внутрішній кут не містить всіх інших вершин на своїх ребрах або у внутрішності.

Опукла оболонка вершин увігнутого багатокутника, а також його ребер, містить зовнішні точки багатокутника.

Примітки
  1. McConnell, Jeffrey J. (2006). Computer Graphics: Theory Into Practice. с. 130. ISBN 0-7637-2250-2.
  2. Leff, Lawrence (2008). Let's Review: Geometry. Hauppauge, NY: Barron's Educational Series. с. 66. ISBN 978-0-7641-4069-3.
  3. Definition and properties of concave polygons with interactive animation.
  4. Chazelle, Bernard; Dobkin, David P. (1985). Optimal convex decompositions. У Toussaint, G.T. Computational Geometry. Elsevier. с. 63–133..

Посилання
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.