Формула площі Гаусса
Формула площі Гаусса (формула землеміра або формула шнурування чи алгоритм шнурування) — формула визначення площі простого багатокутника, вершини якого задано декартовими координатами на площині. Користувач перемножає відповідні координати та складає, щоб знайти область охоплення багатокутника, та віднімає її з багатокутника, що її оточує, аби знайти площу багатокутника всередині. Це зветься формулою шнурування, оскільки додатні й від'ємні складові з координат, що перемножуються, розташовуються на папері хрест-навхрест, як при зав'язуванні шнурків. Її застосовують у геодезії та лісовому господарстві, серед інших галузей.
Формула була написана Мейстером (1724—1788) у 1769 році та Гауссом у 1795 р. Вона може бути перевірена шляхом ділення багатокутника на трикутники, але її також можна розглядати як окремий випадок теореми Гріна.
Формула площі визначається шляхом узяття кожного ребра багатокутника АВ, та обчислення площі трикутника АВО з вершиною на початку координат О, через координати вершин. Обійшовши багатокутник навколо, утворюються трикутники, що містять внутрішню частину багатокутника і розташовані зовні. Різниця між сумою цих площ і є площею самого багатокутника. Тому вона зветься формулою геодезиста, оскільки «картограф» знаходиться на початку координат; якщо він обходить ділянку проти годинникової стрілки, площа додається коли знаходиться ліворуч і віднімається коли праворуч із точки зору на початку координат.
Формула площі є правильною для будь-якого (простого) багатокутника без самоперетинів, який може бути випуклим чи ввігнутим.
Визначення
Формула може бути представлена наступним виразом:
де
- А — площа багатокутника,
- n — кількість сторін багатокутника,
- (xi, yi), i = 1, 2,…, n — координати вершин багатокутника.
Інше представлення цієї ж формули:[1][2]
де xn+1 = x1 і x0 = xn, так само як yn+1 = y1 і y0 = yn.
Якщо точки пронумеровано послідовно в напрямку проти годинникової стрілки, то детермінанти у формулі вище позитивні й модуль у ній може бути опущений; якщо їх пронумеровано в напрямку за годинниковою стрілкою, детермінанти будуть негативними. Це відбувається через те, що формула може розглядатися як окремий випадок теореми Гріна.
Приклади
Для застосування формули необхідно знати координати вершин багатокутника в декартовій площині. Для прикладу візьмемо трикутник із координатами {(2, 1), (4, 5), (7, 8)}. Візьмемо першу х -координату першої вершини й помножимо її на y -координату другої вершини, а потім помножимо х другої вершини на y третьої. Повторимо цю процедуру для всіх вершин. Результат можна визначити за наступною формулою:[3]
де xi і yi позначають відповідну координату. Цю формулу можна отримати, розкривши дужки в загальній формулі для випадку n = 3. За цією формулою можна виявити, що площа трикутника дорівнює половині суми 10 + 32 + 7 − 4 − 35 − 16, що дає 3.
Кількість змінних у формулі залежить від кількості сторін багатокутника. Наприклад, у формулі для площі п'ятикутника будуть використовуватися змінні до x5 і y5:
A для чотирикутника — змінні до x4 та y4:
Складніший приклад
Розглянемо багатокутник, наведений на рисунку й заданий (3,4), (5,11), (12,8), (9,5), (5,6):
.svg.png.webp)
Площа цього багатокутника:
Пояснення назви
Причиною того, що формулу назвали формулою шнурків є загальний метод її обчислення. Цей метод використовує матрицю. У якості прикладу, візьмемо трикутник із вершинами (2,4), (3,-8), і (1,2). Потім збудуємо наступну матрицю, «обходячи колом» трикутник і завершуючи початковою точкою:
Спочатку проведемо діагональ донизу й вправо косою лінією, як зображено нижче:
і перемножимо пари чисел, з'єднаних лінією, а потім складемо всі суми: (2 × −8) + (3 × 2) + (1 × 4) = −6. Зробимо те саме, проводячи косу лінію по діагоналі вгору й вліво, як зображено нижче:
(4 × 3) + (−8 × 1) + (2 × 2) = 8. Потім вирахуємо суму другої групи з першої та візьмемо модуль: |(−6) − (8)| = 14. Ділення результату на два дає площу.
Організація чисел до матриці з діагональними лініями спрощує запам'ятовування формули.
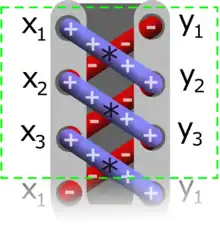
У результаті виконаної операції з рисунками діагональних (косих) ліній матриця з числами нагадує зашнуроване взуття, звідси й походить назва «алгоритму шнурування».
Див. також
Примітки
- Shoelace Theorem, Art of Problem Solving Wiki.
- Weisstein, Eric W. Polygon Area. Wolfram MathWorld. Процитовано 24 липня 2012.
- Richard Rhoad; George Milauskas; Robert Whipple (1991). Geometry for Enjoyment and Challenge (вид. new). McDougal Littell. с. 717–718. ISBN 0-86609-965-4.