Чотирикутник
Чотирикутник — це частина площини, обмежена простою замкненою ламаною, яка містить чотири (4) ланки. Вона складається з чотирьох (4) вершин (точок) і чотирьох сторін (відрізків), що послідовно їх сполучають. При цьому жодні три з даних точок не повинні лежати на одній прямій. Вершини чотирикутника називаються сусідніми, якщо вони є кінцями однієї з його сторін. Несусідні вершини називаються протилежними. Відрізки, що сполучають протилежні вершини чотирикутника, називаються діагоналями.
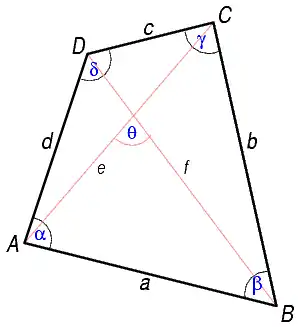
У чотирикутнику на зображені 1 діагоналями є відрізки AC і BD.
Сторони чотирикутника, що виходять з однієї вершини, називаються сусідніми сторонами. Сторони, які не мають спільного кінця, називаються протилежними сторонами. У чотирикутнику на даному малюнку протилежними сторонами є сторони AB і CD, BC і AD. Чотирикутник позначають, записуючи його вершини. Наприклад, чотирикутник на зображені 1 позначено так: ABCD. У позначенні чотирикутника вершини, що стоять поряд, повинні бути сусідніми. Чотирикутник ABCD можна також позначити BCDA або DCBA. Але не можна позначити ABDC (B і D — не сусідні вершини).
Внутрішні кути простого чотирикутника ABCD мають в сумі 360 градусів, тобто
Сума довжин усіх сторін чотирикутника називається периметром.
Прості чотирикутники
Будь-який чотирикутник, сторони якого не перетинаються є простим чотирикутником.
Опуклі чотирикутники
В опуклих чотирикутників всі внутрішні кути є меншими за 180°, а дві діагоналі знаходяться в середині чотирикутника.
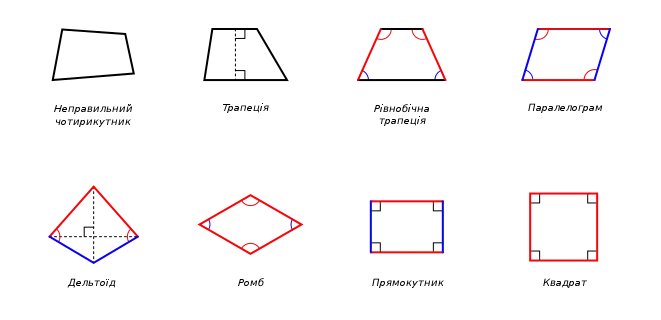
- Неправильний чотирикутник: не має паралельних сторін.
- Трапеція: одна пара протилежних сторін є паралельною.
- Рівнобічна трапеція: одна пара протилежних сторін є паралельними, а кути нахилу сторін при основі є рівними. Альтернативними визначеннями є: чотирикутник що має вісь симетрії, яка перетинає пару протилежних сторін, або трапеція із діагоналями рівної довжини.
- Паралелограм: чотирикутник із двома парами паралельних сторін. еквівалентною умовою є те, що його протилежні сторони мають однакову довжину; що протилежні кути рівні; або що діагоналі перетинаються і ділять одна одну навпіл. До паралелограмів відноситься ромб, прямокутник, а також квадрат.
- Ромб: всі чотири сторони мають однакову довжину. Або еквівалентно: діагоналі перпендикулярні і перетином ділять навпіл одна одну. Не формально це є «сплюснутий квадрат» (але строго математично квадрат теж є ромбом).
- Ромбоїд: паралелограм в якого суміжні сторони мають різні довжини а деякі кути тупими (не має прямих кутів). Деякі джерела називають його паралелограмом, що не є ромбом.[1]
- Прямокутник: всі чотири кути є прямими кутами. Еквівалентно: діагоналі мають однакову довжину і при перетині діляться навпіл. До прямокутників відноситься і квадрат.
- Квадрат (правильний прямокутник): всі чотири сторони мають однакову довжину, а чотири кути є прямими. Діагоналі перетинають одна одну навпіл і під прямим кутом, а також мають однакову довжину. Чотирикутник є квадратом тоді і лише тоді, коли він одночасно є ромбом і прямокутником (чотири рівні сторони і чотири однакові кути).
- Дельтоїд: дві пари прилеглих сторін мають однакову довжину. З цього випливає, що одна з діагоналей розділяє дельтоїд на конгруентні трикутники, і два кути між парами нерівних сторін мають однакову величину. Також, його діагоналі є перпендикулярними. До дельтоїдів відноситься ромб.
- Описаний чотирикутник: чотири сторони є дотичними до вписаного кола. Опуклий чотирикутник може описати коло тоді і лише тоді коли суми його протилежних сторін рівні.
- Описана трапеція: трапеція, чотири сторони якої є дотичними до вписаного кола.
- Вписаний чотирикутник: чотири вершини лежать на описаному колі. Опуклий чотирикутник є вписаним, тоді і тільки тоді коли суми протилежних кутів дорівнюють 180°.
- Прямокутний дельтоїд: дельтоїд, дві протилежні кути якого є прямими. Він є одним із видів вписаних чотирикутників.
- Біцентричний чотирикутник: чотирикутник, який одночасно є вписаним у коло і описаним колом.
- Ортодіагональний чотирикутник: діагоналі перетинаються під прямим кутом.
- Зовнішньо-описаний чотирикутник: продовження чотирьох сторін є дотичними до зовнішнього кола.
Увігнуті чотирикутники
В увігнутих чотирикутників, один із внутрішніх кутів є більшим за 180° а одна із двох діагоналей лежить за межами чотирикутника.
Складні чотирикутники

До складних чотирикутників відносять не правильні чотирикутники, грані яких перетинаються. Такі чотирикутники перетинають самі себе і мають ряд не формальних назв: перехрещений чотирикутник, чотирикутник-метелик або бантик. Сума внутрішніх кутів перехрещеного чотирикутника буде дорівнювати 720°, а два внутрішні кути в ньому є розгорнутими і знаходяться ззовні. Тобто перехрещеного чотирикутника, чотири «внутрішні» кути знаходяться по обидві сторони перетину (два гострих і два розгорнутих, всі з лівої сторони або з правою, в залежності від того в якому порядку перераховуються).[2]
- Перехрещена трапеція[3]: перехрещений чотирикутник, в якому (як у трапеції) одна пара не суміжних сторін є паралельною
- Антипаралелограм: перехрещений чотирикутник в якого (як в паралелограма) кожна пара не суміжних сторін мають однакову довжину.
- Перехрещений прямокутник: це антипаралелограм, сторонами якого є дві протилежні сторони і дві діагоналі звичайного прямокутника, таким чином від має одну пару протилежних сторін, що є паралельними.
- Перехрещений квадрат: особливий випадок перехрещеного прямокутника, в якого дві сторони перетинаються під прямими кутами.
Повний чотирибічник
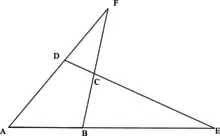
Хоча така назва може бути еквівалентна чотирикутнику, в неї часто вкладають додатковий сенс. Четвірка прямих, ніякі дві з яких не паралельні і ніякі три не проходять через одну точку, називається повним чотирибічником. Така конфігурація зустрічається в деяких твердженнях евклідової геометрії (наприклад, теорема Менелая, пряма Ньютона - Гауса, пряма Обера, Теорема Мікеля тощо), в яких часто всі прямі є взаємозамінними.
Особливі відрізки
Двома діагоналями опуклого чотирикутника є відрізки, що сполучають протилежні вершини.
Двома бімедіанами (англ. bimedians) опуклого чотирикутника є відрізки, що сполучають середини протилежних сторін[4]. Вони перетинаються у точці, яка називається «центроїдом» вершин чотирикутника.
Також в опуклому чотирикутнику бівисотою (англ. maltitude) будемо називати висоту, яка має основу у середині протилежної сторони[5]. Всього у чотирикутнику можна провести чотири бівисоти.
Площа
Існує декілька загальних формул розрахунку площі S опуклого чотирикутника ABCD із сторонами a = AB, b = BC, c = CD і d = DA.
Тригонометричні формули
Площа чотирикутника може бути задана за допомогою тригонометричних функцій наступним чином:
де довжини кожної діагоналі задані як e і f, а кут між ними дорівнює θ.[6] У випадку коли діагоналі перпендикулярні (тобто для ромба, квадрата і дельтоїда), ця формула спрощується до оскільки θ дорівнює 90°.
Площу можна розрахувати через бімедіани наступним чином[7]
Де довжини медіан дорівнюють m і n, а кут між ними дорівнює φ.
Формула Бретшнайдера[8] визначає площу черед дві сторони і два протилежних кута:
де сторони відповідно задані як a, b, c, d, і де s є півпериметром, а A і C є двома (будь-якими) протилежними кутами. Для вписаного чотирикутника цей вираз спрощується до формули Брамагупти, оскільки A + C = 180°.
Іншою формулою для розрахунку площі через кути і сторони, де кут C знаходиться між сторонами b і c, а кут A між сторонами a та d, є
У випадку із вписаним чотирикутником, остання формула скорочується до
Для паралелограма, де обидві пари протилежних сторін і кутів є рівними, ця формула в свою чергу спрощується до виразу
Альтернативним чином, можна визначити площу чотирикутника через сторони і кут перетину його діагоналей θ, для тих випадків доки цей кут не дорівнює 90°:[9]
У випадку з паралелограмом, остання формула буде виглядати як
Іншою формулою, що містить сторони a, b, c, d є[7]
де x є відстанню між середніми точками діагоналей, а φ є кутом між бімедіанами.
І ще однією тригонометричною формулою, що містить сторони a, b, c, d і кут α між a і b є:
що може використовуватися і як площа увігнутого чотирикутника (що має увігнуту частину протилежну до кута α) змінивши перший знак + на -.
Не-тригонометричні формули
Дві наступні формули задають площу S чотирикутника через сторони a, b, c, d, напівперіметр s, і діагоналі e, f:
Перше рівняння зводиться до формули Брахмагупти для вписаного чотирикутника, оскільки в такому випадку ef = ac + bd.
Площу також можна задати через бімедіани m, n і діагоналі e, f:
Насправді, будь-яке з трьох значень m, n, e, і f є достатнім для визначення площі, оскільки для будь-якого чотирикутника ці чотири значення пов'язані рівнянням [14] Відповідними спрощеними виразами будуть наступні рівняння для розрахунку площі:[15]
якщо дані довжини двох бімедіан і діагональ, і[15]
якщо відомі довжини двох діагоналей і одна бімедіана.
Векторна форма
Площу чотирикутника ABCD можна розрахувати за допомогою векторів. Нехай вектори AC і BD утворюють діагоналі від A до C і від B до D. Площа чотирикутника тоді дорівнюватиме
що є половиною величини векторного добутку векторів AC і BD. У двовимірному Евклідовому просторі, вектор AC можна задати у вигляді вектора у Декартовому просторі як (x1,y1) і вектор BD як (x2,y2), тому рівняння можна переписати наступним чином:
Теореми
- Добутки площ трикутників, утворених частинами діагоналей від їх країв до їх перетину і протилежними сторонами чотирикутника, рівні.
- Сума кутів опуклого чотирикутника дорівнює 360°.
- У будь-якому вписаному чотирикутнику суми протилежних кутів дорівнють 180°.
- У будь-якому описаному чотирикутнику суми протилежних сторін рівні.
Діагоналі
Довжина діагоналей
Довжини діагоналей опуклого чотирикутника ABCD із відповідними вершинами A, B, C, D і сторонами a = AB, b = BC, c = CD, і d = DA, довжини діагоналей p = AC і q = BD можна розрахувати за допомогою теореми косинусів для кожного трикутника, що утворені діагоналями і двома сторонами чотирикутника. Таким чином
і
Інші, більш симетричні формули для знаходження довжин діагоналей:[16]
і
Узагальнення правила паралелограма і теореми Птолемея
Для будь-якого опуклого чотирикутника ABCD, сума квадратів чотирьох сторін дорівнює сумі квадратів двох діагоналей плюс чотири квадрати лінійного сегменту, що сполучає середні точки діагоналей. Тобто
де x це відстань між середніми точками діагоналей.[14] Це рівняння відоме як теорема Ейлера про чотирикутник і є узагальненням для правила паралелограма.
Німецький математик Карл Антон Бретшнейдер в 1842 вивів наступне узагальнення для теореми Птолемея, стосовно добутку діагоналей опуклого чотирикутника[17]
Це рівняння можна вважати аналогічним до теореми косинусів для чотирикутника. Для вписаного чотирикутника, в якого , це рівняння спрощується до pq = ac + bd. Оскільки , таким чином, це також доводить нерівність Птолемея.
Бімедіани
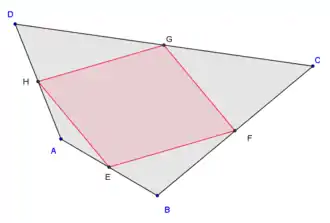
Бімедіанами чотирикутника є такі лінійні відрізки, що сполучають середні точки його протилежних сторін. Перетином бімедіан є центроїд вершин чотирикутника.[18]
Середні точки будь-якого чотирикутника (опуклого, увігнутого або перехрещеного) є вершинами паралелограма, що називається паралелограмом Варіньона. Він має наступні властивості:
- Кожна пара протилежних сторін паралелограма Варіньона є паралельними діагоналі початкового чотирикутника.
- Сторона паралелограма Варіньона має довжину, що дорівнює половині довжини діагоналі початкового чотирикутника до якої ця сторона є паралельною.
- Площа паралелограма Варіньона дорівнює половині площі початкового чотирикутника. Це є вірним для опуклих, увігнутих і перехрещених чотирикутників, де площа останнього задається як різниці площ трикутників з яких він складається.[19]
- Периметр паралелограма Варіньона дорівнює сумі довжин діагоналей початкового чотирикутника.
- Діагоналі паралелограма Варіньона є бімедіанами початкового чотирикутника.
Дві бімедіани чотирикутника і лінійні відрізки, що сполучають середні точки діагоналей в тому чотирикутнику є конкурентними прямими і всі поділяються навпіл точкою їх перетину.[14]
Для опуклого чотирикутника із сторонами a, b, c і d, довжина бімедіани, що сполучає середні точки сторін a і c дорівнюватиме
де p і q є довжинами діагоналей.[20] Довжина бімедіани, що сполучає середні точки сторін b і d дорівнює
Отже[14]
Це також є наслідком застосування правила паралелограма до паралелограма Варіньона.
Довжину бімедіан також можна виразити через дві протилежні сторони і відстань x між середніми точками діагоналей. Це можна отримати застосувавши теорему Ейлера для чотирикутників щодо вищезгаданих формул. Звідки отримаємо[13]
і
Зверніть увагу, що дві протилежні сторони в цих формулах не є тими двома сторонами, що сполучає бімедіана.
Для опуклого чотирикутника є справедливим наступний дуальний взаємозв'язок між бімедіанами і діагоналями:[21]
- Дві бімедіани мають однакову довжину тоді і лише тоді, коли дві діагоналі є перпендикулярними.
- Дві бімедіани є перпендикулярними, толі і лише тоді, коли дві діагоналі мають однакову довжину.
Тригонометричні тотожності
Чотири кути простого чотирикутника ABCD задовольняють наступним рівнянням:[22]
і
Також,[23]
В двох останніх формулах, жоден з кутів не може бути прямим кутом, оскільки тангенс 90° є не визначеним.
Нерівності
Площа
Якщо опуклий чотирикутник має сторони a, b, c, d і діагоналі p, q, тоді його площа S задовольняє нерівностям[24]
- , що буде рівністю лише для прямокутника.
- , що буде рівністю лише для квадрата.
- , що буде рівністю лише якщо дві діагоналі є перпендикулярними і мають однакову довжину.
- , що є рівністю лише для прямокутника.[7]
Із формули Бретшнайдера прямо випливає, що площа чотирикутника задовольнятиме нерівності
що буде рівністю тоді й лише тоді коли чотирикутник є вписаним чотирикутником або виродженим, тобто таким що довжина однієї зі сторін дорівнюватиме сумі довжин інших трьох (тобто він перетворився у відрізок, тому його площа дорівнює нулю).
Площа будь-якого чотирикутника також задовольнятиме нерівності[25]
Позначивши периметр чотирикутника як L, матимемо наступне[25]
що буде рівністю лише для випадку із квадратом.
Площа опуклого чотирикутника також задовольняє:
де довжини діагоналей задані як p і q, що буде рівністю лише за умови, що діагоналі перпендикулярні одна одній.
Діагоналі і бімедіани
Наслідком із теореми Ейлера про чотирикутники є наступна нерівність
де рівність буде справедливою, тоді й тільки тоді коли чотирикутник є паралелограмом.
Ейлер також узагальнив теорему Птолемея, що є рівністю для вписаного чотирикутника, у нерівність для опуклого чотирикутника. Нерівність задає наступне:
що буде рівністю тоді й лише тоді, коли чотирикутник є вписаним.[14].
В опуклому багатокутнику бімедіани m, n і діагоналі p, q пов'язані між собою нерівністю
де рівність буде справедливою тоді і лише тоді, коли діагоналі є рівними.[26] Це прямо випливає із рівності для чотирикутника
Просторові чотирикутники
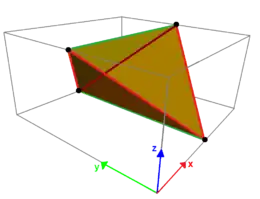
Чотирикутник, що не знаходиться в площині називається просторовим чотирикутником або косим чотирикутником. Формули для розрахунку його двогранних кутів при відомих довжинах ребер і кутів між двома прилеглими ребрами були отримані при вивчені властивостей молекул, таких як молекули циклобутана, які містять «замкнуте» кільце із чотирьох атомів.[28][29] Косий чотирикутник разом із своїми діагоналями утворює (не обов'язково правильний) тетраедр, і навпаки, кожен косий чотирикутник утворений із тетраедра, в якого усунута пара протилежних ребер.
Див. також
Примітки
- Archived copy. Архів оригіналу за 14 травня 2014. Процитовано 20 червня 2013.
- Stars: A Second Look
- Butler, David (6 квітня 2016). The crossed trapezium. Making Your Own Sense. Процитовано 13 вересня 2017.
- E.W. Weisstein. Bimedian. MathWorld – A Wolfram Web Resource.
- E.W. Weisstein. Maltitude. MathWorld – A Wolfram Web Resource.
- Harries, J. "Area of a quadrilateral, " Mathematical Gazette 86, July 2002, 310—311.
- Josefsson, Martin (2013). Five Proofs of an Area Characterization of Rectangles. Forum Geometricorum 13: 17–21..
- R. A. Johnson, Advanced Euclidean Geometry, 2007, Dover Publ., p. 82.
- Mitchell, Douglas W., "The area of a quadrilateral, " Mathematical Gazette 93, July 2009, 306—309.
- J. L. Coolidge, «A historically interesting formula for the area of a quadrilateral», American Mathematical Monthly, 46 (1939) 345—347.
- E.W. Weisstein. Bretschneider's formula. MathWorld – A Wolfram Web Resource.
- Archibald, R. C., «The Area of a Quadrilateral», American Mathematical Monthly, 29 (1922) pp. 29–36.
- Josefsson, Martin (2011). The Area of a Bicentric Quadrilateral. Forum Geometricorum 11: 155–164..
- Altshiller-Court, Nathan, College Geometry, Dover Publ., 2007.
- Josefsson, Martin (2016) ‘100.31 Heron-like formulas for quadrilaterals’, The Mathematical Gazette, 100 (549), pp. 505—508.
- Rashid, M. A. & Ajibade, A. O., "Two conditions for a quadrilateral to be cyclic expressed in terms of the lengths of its sides", Int. J. Math. Educ. Sci. Technol., vol. 34 (2003) no. 5, pp. 739–799.
- Andreescu, Titu & Andrica, Dorian, Complex Numbers from A to…Z, Birkhäuser, 2006, pp. 207—209.
- Weisstein, Eric W. "Quadrilateral." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/Quadrilateral.html
- H. S. M. Coxeter and S. L. Greitzer, Geometry Revisited, MAA, 1967, pp. 52–53.
- Mateescu Constantin, Answer to Inequality Of Diagonal
- Josefsson, Martin (2012). Characterizations of Orthodiagonal Quadrilaterals. Forum Geometricorum 12: 13–25..
- C. V. Durell & A. Robson, Advanced Trigonometry, Dover, 2003, p. 267.
- MathPro Press, "Original Problems Proposed by Stanley Rabinowitz 1963–2005", p. 23,
- O. Bottema, Geometric Inequalities, Wolters–Noordhoff Publishing, The Netherlands, 1969, pp. 129, 132.
- Alsina, Claudi; Nelsen, Roger (2009). When Less is More: Visualizing Basic Inequalities. Mathematical Association of America. с. 68..
- Josefsson, Martin (2014). Properties of equidiagonal quadrilaterals. Forum Geometricorum 14: 129–144.
- Inequalities proposed in “Crux Mathematicorum”, .
- Barnett, M. P.; Capitani, J. F. (2006). Modular chemical geometry and symbolic calculation. International Journal of Quantum Chemistry 106 (1): 215–227. doi:10.1002/qua.20807.
- Hamilton, William Rowan (1850). On Some Results Obtained by the Quaternion Analysis Respecting the Inscription of "Gauche" Polygons in Surfaces of the Second Order. Proceedings of the Royal Irish Academy 4: 380–387.
Джерела
- Великий довідник школяра: 5-11 класи — Харків: Школа, 2003, ISBN 966-8114-20-5