Фібоначчієва купа

Купа Фібоначчі — структура даних, ефективна реалізація черги з пріоритетом.

Операція	Амортизаційний час
Make-Heap	$\Theta (1)$
Insert	$\Theta (1)$
Minimum	$\Theta (1)$
Extract-Min	$O(\lg n)$
Union	$\Theta (1)$
Decrease-Key	$\Theta (1)$
Delete	$O(\lg n)$

З теоретичної точки зору купи Фібоначчі особливо варто використовувати, коли кількість Extract-Min і Delete операцій мала порівняно з кількістю інших операцій. Наприклад, деякі алгоритми на графах можуть викликати Decrease-Key на кожному ребрі. Для щільного графу сталий амортизаційний час $\Theta (1)$ кожного виклику Decrease-Key складається у велику перевагу в порівнянні з логарифмічним часом $\Theta (\lg n)$ у найгіршому випадку в бінарній купі. Це можна побачити на прикладі алгоритмів про найкоротші шляхи з одного входу і мінімального кістякового дерева. З практичної точки зору сталий множник прихований у складності алгоритму і складність у програмуванні купи Фібоначчі роблять її менш бажаною, ніж звичайну бінарну або d-арну купу для більшості застосувань.

Історія

Фібоначчієву купу запропонували Фредман і Тар'ян у 1984 році. Головним гаслом цієї конструкції було «ми виконуємо роботу лише коли мусимо, і тоді ми використовуємо це для спрощення структури настільки наскільки можливо, таким чином, щоб майбутня робота була легкою».

Структура купи

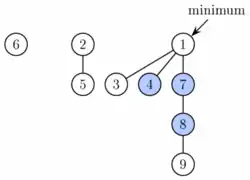
Зображення 1. Приклад Фібоначчієвої купи. Купа має три дерева степенів 0, 1 і 3. Три позначені вершини (синім). Отже, потенціал купи становить 9 (3 дерева + 2 × (3 позначених-вершини)).

Купа Фібоначчі являє собою набір дерев, кожне з яких є мінкупою змінної арності з такими властивостями:

Вузли дерев відповідають елементам, що зберігаються в черзі.
Корені куповпорядкованих дерев поєднані у двобічно зв'язаний список.
Зберігається вказівник на корінь дерева, який відповідає елементу з найменшим ключем (варто зауважити, що те, що кожне дерево є мінкупою, гарантує, що цей елемент буде коренем одного з дерев).
Для кожного вузла зберігається його ранг (степінь), тобто кількість його дітей, а також чи він позначений (мету позначення ми визначимо пізніше).
Вимога розміру: якщо вузол u має степінь k, то піддерево з коренем u має щонайменше $F_{k+2}$ вузлів, де $F_{i}$ — це i-те число Фібоначчі, тобто $F_{0}=0,F_{1}=1$ і $F_{i}=F_{i-1}+F_{i-2}$ для $i\geq 2.$

Кожен вузол x містить вказівник x.p на свого предка і вказівник x.child на один із його нащадків. Нащадки зв'язані в циклічний двобічно зв'язаний список. Кожен нащадок y має вказівники y.left та y.right. Якщо вузол є єдиним нащадком, тоді y = y.left = y.right. Нащадки елемента можуть перебувати у будь-якому порядку. Використання двобічно зв'язаних списків уможливлює вставляння і видалення елементів за час O(1), а також зв'язування двох списків за O(1). Також кожен вузол має атрибут x.degree, що дорівнює кількості нащадків, і атрибут x.mark, що показує, чи втратив вузол нащадка з моменту, як він став нащадком свого поточного предка.

Доступ до купи відбувається через вказівник H.min, який вказує на корінь дерева з найменшим ключем. Якщо дерево порожнє, то H.min дорівнює NIL.

Для оцінки швидкості використовують метод потенціалів із потенціальною функцією $\Phi (H)=t(H)+2m(H).$ Де $t(H)$ дає кількість дерев у купі, а $m(H)$ — кількість позначених вузів.

Максимальний степінь

Надалі вважатимемо, що нам відома верхня межа D(n) максимального степеня вузла у Фібоначчієвій купі з n вузлами. Якщо купа підтримує лише операції поєднуваної купи, тоді $D(n)\leq \lfloor \lg n\rfloor .$ Хоча, навіть якщо Фібоначчієва купа підтримує Decrease-Key та Delete, то $D(n)=O(\lg n).$

Операції

INSERT

Вставка дужа проста: додаємо новий елемент s як нову мінкупу в колекцію і перевіряємо, чи k(s) менше за поточне найменше значення. Якщо так, то відповідно змінюємо вказівник H.min.

Insert(H, x)
 1 x.degree = 0
 2 x.p = NIL 
 3 x.child = NIL
 4 x.mark = FALSE
 5 якщо H.min == NIL
 6     створити список коренів для H, що містить лише x
 7     H.min = x
 8 інакше вставити x у список коренів H
 9     якщо x.key < H.min.key
10         H.min = x
11 H.n = H.n + 1

Щоб визначити амортизаційну вартість вставляння елемента, нехай H буде початковою Фібоначчієвою купою і H' буде результовною. Тоді $t(H')=t(H)+1$ і $m(H')=M(H),$ отже збільшення потенціалу становить

((t(H)+1)+2m(H))-(t(H)+2m(H)))=1.

Оскільки амортизаційна вартість дорівнює сумі дійсної вартості і різниці потенціалів, то вона дорівнює $O(1)+1=O(1).$

DECREASE-KEY

Фібоначчієва купа із зображення 1 після зменшення ключа з 9 до 0. Цей вузол, як і два його позначені попередники, відтинаються від дерева з коренем 1 і розташовуються як нові корені.

Коли ми зменшуємо ключ елемента s, якщо умови мінкупи все ще задовільняються, то нам більше не потрібно робити нічого. Інакше, ми просто відтинаємо піддерево з коренем в s і вставляємо його як нове піддерево у колекцію. Ми порівнюємо новий ключ s із попереднім мінімальним елементом і змінюємо вказівник H.min відповідно.

Таким чином, ми отримуємо щось, що виглядає подібно до бажаної Фібоначчієвої купи. Однак, проблема із простим відтинанням кожного такого s полягає в тому, що ми можемо врешті решт порушити вимогу розміру. Отже, щоб полегшити ситуацію, ми впроваджуємо додаткове правило, що коли ми відтинаємо s ми перевіряємо, чи не помічений його батьківський елемент. Якщо так, то ми також відтинаємо батьківській елемент і знімаємо позначку з нього. Інакше, ми просто позначаємо батьківський елемент. Перевірка батьківського елемента виконується рекурсивно, тобто, якщо батько батька позначений, ми відтинаємо і його також. Очевидно, що якщо ми відтинаємо корінь, то ми не робимо нічого, тому немає сенсу позначати корінь. Тому, ця потенційно каскадна процедура, завжди завершується.

Decrease-Key(H,x,k)
1 якщо k > x.key
2     помилка "новий ключ більший ніж попередній"
3 x.key = k
4 y = x.p
5 якщо y != NIL і x.key < y.key
6     Cut(H,x,y)
7     Cascading-Cut(H,y)
8 якщо x.key < H.min.key
9     H.min = x

Cut(H,x,y)
1 видалити x зі списку дітей y, зменшити y.degree
2 додати до списку коренів H
3 x.p = NIL
4 x.mark = FALSE

Cascading-Cut(H,y)
1 z = y.p
2 якщо z != NIL
3     якщо y.mark == FALSE
4         y.mark = TRUE
5     інакше Cut(H,y,z)
6            Cascading-Cut(H,z)

З'ясуємо дійсну вартість зменшення ключа. Decrease-Key потребує O(1), не враховуючи каскадного видалення. Припустимо, що відбулось c викликів Cascading-Cut. Виконання кожного Cascading-Cut, не враховуючи рекурсивних викликів, потребує O(1). Отже дійсна вартість Decrease-Key становить O(c).

Тепер обчислимо різницю потенціалів. У висліді зменшення ключа утворюється c-1 нових дерев через каскадні відтинання і дерево з коренем x. c-1 вузів припиняють бути позначеними. І, можливо, позначається один вузол.

((t(H)+c)+2(m(H)-c+2))-(t(H)+2m(H))=4-c.

З цього випливає, що амортизаційна вартість буде не більше ніж

O(c)+4-c=O(1).

EXTRACT-MIN

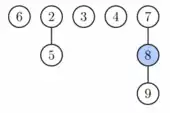
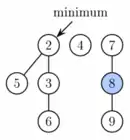
Фібоначчієва купа із зображення 1 після першої фази вилучення мінімального елемента. Вузол з ключем 1 (мінімум) було видалено і його діти були додані як окремі дерева.

Фібоначчієва купа із зображення 1 після виконання вилучення найменшого елемента. Спершу, поєднані вузли 3 і 6. Потім результат поєднаний із деревом з коренем у вузлі 2. Насамкінець, знайдено новий мінімум.

Насамкінець, ми можемо описати видобування мінімального елемента s*. Починаємо з видалення s* (на нього вказує H.min) і додавання усіх його дітей як дерев у колекцію. Тепер, ми продивляємось усю колекцію, знаходимо найменший елемент і оновлюємо H.min відповідно.

На цьому можна було б і завершити, оскільки ми отримали правильну Фібоначчієву купу. Однак, не складно побачити, що досі описані операції над купою, роблять список коренів довшим і довшим. Отже, проходження через увесь список коренів ставатиме обчислювально дорожчим. Отже, якщо ми вже маємо зробити якусь роботу у будь-якому випадку, то ми виконаємо очищення зараз, щоб уникнути більшої роботи у наступному. Тому, доти доки наявні два дерева з однаковим рангом, скажімо k, ми зливаємо ці дерева, щоб отримати дерево рангу k+1. Злиття полягає у порівнянні коренів і додавання дерева з більшим коренем як дочірнього до другого кореня. Зауважимо, що оскільки злиття може створити друге дерево рангу k+1 у колекції, один корінь може взяти участь у кількох злиттях.

Extract-Min(H)
 1 z = H.min
 2 якщо z != NIL
 3     для кожної дитини x z
 4         додати x до списку коренів H
 5         x.p = NIL
 6     видалити z зі списку коренів H
 7     якщо z == z.right // Вважаємо, що видалення z із двобічного списку не змінює її right/left вказівників
 8         H.min = NIL
 9     інакше H.min = z.right
10         Consolidate(H)
11     H.n = H.n - 1
12 повернути z

Після видалення z ми консолідуємо список коренів H. Консолідація відбувається виконуючи наступні кроки допоки у списку коренів присутні корені з однаковим степенем.

Знайти два корені x, y з однаковим степенем. Припустимо, без втрати загальності, що x.key =< y.key.
Приєднуємо y до x. Тут ми збільшуємо x.degree і очищаємо позначку на y.

Consolidate(H)
 1 нехай A[0..D(H.n)] буде новим масивом
 2 для i = 0 до D(H.n)
 3     A[i] = NIL
 4 для кожного вузла w у списку коренів H
 5     x = w
 6     d = x.degree
 7     поки A[d] != NIL
 8         y = A[d] // Інший корінь з тим самим степенем як і x
 9         якщо x.key > y.key
10             обміняти x і y
11         Heap-Link(H,y,x)
12         A[j] = NIL
13         d = d + 1
14     A[d] = x
15 H.min = NIL
16 для i = 0 до D(H.n)
17     якщо A[i] != NIL
18         якщо H.min == NIL
19             створити список коренів для H, що містить лише A[i]
20             H.min = A[i]
21         інакше вставити A[i] у список коренів H
22             якщо A[i].key < H.min.key
23                H.min = A[i]

Heap-Link(H,y,x)
1 видалити y зі списку коренів H
2 зробити y дочірнім для x, збільшити x.degree
3 y.mark = FALSE

Обчислимо дійсну вартість видобування найменшого елемента. O(D(n)) маємо завдяки Extract-Min, через необхідність обробити усі дочірні вузли, і завдяки циклам 2-3 і 16-23 у Consolidate. Розглянемо внесок циклу 4-14 Consolidate, для цього використаємо груповий аналіз. Розмір списку коренів перед викликом Consolidate не більше ніж D(n) + t(H) + 1. Ми знаємо, що кожен раз у тілі циклу while один з коренів приєднується до іншого, отже, загальна кількість ітерацій циклу while у всіх ітераціях зовнішнього циклу for не може перевищити розмір списку коренів. Тому загальна кількість роботи у циклі 4-14 щонайбільше пропорційна до D(n) + t(H). Отже, всього нам треба O(D(n) + t(H)).

Потенціал перед видобуванням мінімального вузла є t(H) + 2m(H), а після — не більше ніж D(n) + 1. З цього і дійсної вартості маємо амортизаційну вартість

O(D(n)+t(H))+((D(n)+1)+2m(H))-(t(H)+2m(H))=O(D(n))+O(t(H))-t(H)=O(D(n)).

Обмеження на найбільший степінь

Лема. Нехай  $x$  це вузол, і нехай  $y_{1},\dots ,y_{k}$  позначають його дітей у порядку в якому вони були додані до  $x.$  Тоді:
 $y_{i}.degree\geq {\begin{cases}0&i=1\\i-2&i\geq 1\end{cases}}$ 
Доведення: 
Очевидно, що y₁.degree ≥ 0. Для i ≥ 2, коли ми y_i додавали до x, там вже було щонайменше i-1 дочірніх елементів, значить на момент додавання степінь y_i мав дорівнювати степеню x. З того часу один з дочірніх елементів y міг бути відрізаним. Отже, степінь y_i міг зменшитись на 1 і стати i-2.∎

Факти про числа Фібоначчі: 
1.  $\forall k\geq 0,F_{k+2}=1+\sum _{i=0}^{k}F_{i}.$ 
2.  $\forall k\geq 0,F_{k+2}\geq \phi ^{k},$  де  $\phi =(1+{\sqrt {5}})/2.$

Лема. Нехай x буде вузлом у купі Фібоначчі і нехай k = x.degree. Тоді size(x) ≥ F_k+2 ≥ φ^k.

Наслідок: Найбільший степінь D(n) будь-якого вузла в n-вузловій Фібоначчієвій купі є O(lg n).
Доведення: Нехай x буде довільним вузлом і k=x.degree. Маємо, що n ≥ size(x) ≥ φ^k. Логарифмуючи з основою φ отримуємо k ≤ log_φ n. Оскільки k ціле, то  $k\leq \lfloor \log _{\phi }n\rfloor .$ ∎

Джерела

Томас Кормен; Чарльз Лейзерсон, Рональд Рівест, Кліфорд Стайн (2009) [1990]. 19 Fibonacci Heaps. Вступ до алгоритмів (вид. 3rd). MIT Press і McGraw-Hill. с. 505–530. ISBN 0-262-03384-4.
Fibonacci Heaps на www.cs.princeton.edu

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.